题目内容
13.如图(a)所示,一个电阻值为R,匝数为n的圆形金属线圈与阻值为2R的电阻R1连结成闭合回路,a、b端点通过导线与水平放置、间距为d的平行金属板相连.线圈的半径为r1.在线圈中半径为r2的圆形区域存在垂直于线圈平面向里的匀强磁场,磁感应强度B随时间t变化的关系图线如图(b)所示.图线与横、纵轴的截距分别为t0和B0.导线的电阻不计.在0至t1时间内:
(1)求通过电阻R1上的电流方向;
(2)求通过电阻R1上的电流大小;
(3)一质量为m的带电微粒水平射入金属板间,恰能匀速通过,试判断该微粒带何种电荷?带电量为多少?(重力加速度为g).
分析 (1)根据楞次定律判断感应电流的方向;
(2)根据法拉第电磁感应定律判断感应电动势的大小,然后结合闭合电路欧姆定律列式求解决感应电流的大小;
(3)微粒匀速通过电场区,电场力与重力平衡,根据平衡条件列式求解即可.
解答 解:(1)由楞次定律可判断通过电阻R1上的电流方向为从b到a;
(2)由图(b)可知,0至t1时间内,磁感应强度的变化率:
$\frac{△B}{△t}=\frac{{B}_{0}}{{t}_{0}}$ ①
由法拉第电磁感应定律有:
E=n$\frac{△∅}{△t}$=n$\frac{△B}{△t}S$ ②
而S=$π{r}_{2}^{2}$ ③
由闭合电路欧姆定律有:
I1=$\frac{E}{{R}_{1}+R}$ ④
联立以上各式解得,通过电阻R1上的电流大小为:
I1=$\frac{n{B}_{0}π{r}_{2}^{2}}{3R{t}_{0}}$ ⑤
(3)由于金属板间的电场强度方向向上,带电微粒所受电场力与场强方向相同,带正电.
设带电微粒带电量为q,有:
mg=qE1 ⑥
金属板两板间电压:
U=I1R1 ⑦
电场强度大小:
E1=$\frac{U}{d}$ ⑧
⑤~⑧式联立,得:
q=$\frac{3mgd{t}_{0}}{2n{B}_{0}π{r}_{2}^{2}}$
答:(1)通过电阻R1上的电流方向为从b到a;
(2)通过电阻R1上的电流大小为$\frac{n{B}_{0}π{r}_{2}^{2}}{3R{t}_{0}}$;
(3)该微粒带正电荷,电量为$\frac{3mgd{t}_{0}}{2n{B}_{0}π{r}_{2}^{2}}$.
点评 本题是力电综合问题,要明确电路结构,根据法拉第电磁感应定律列式求解感应电动势、根据闭合电路的欧姆定律列式求解电流强度,根据平衡条件求解电荷的带电量.

| A. | 伽利略、开普勒 | B. | 开普勒、牛顿 | C. | 牛顿、卡文迪许 | D. | 伽利略、牛顿 |
| A. | $\frac{{{U}_{1}}^{2}}{R}$ | B. | $\frac{({U}_{1}-{U}_{2})^{2}}{R}$ | C. | I2R | D. | U1I |
 大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随轮的转动而做匀速圆周运动,对此有以下说法,其中正确的是( )
大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随轮的转动而做匀速圆周运动,对此有以下说法,其中正确的是( )| A. | 游客处于一种平衡状态 | |
| B. | 游客做的是一种变加速曲线运动 | |
| C. | 游客做的是一种匀变速运动 | |
| D. | 游客的速度和加速度都在不断地改变着 |
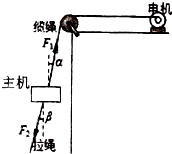 如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )
如图所示,高层住宅外安装空调主机时,电机通过缆绳牵引主机沿竖直方向匀速上升.为避免主机与阳台、窗户碰撞,通常会用一根拉绳拽着主机,地面上拽拉绳的人通过移动位置,使拉绳与竖直方向的夹角β保持不变.则在提升主机过程中(题中缆绳和拉绳均视为轻质绳),下列结论正确的是( )| A. | 缆绳拉力F1和拉绳拉力F2都增大 | |
| B. | 缆绳拉力F1和拉绳拉力F2都不变 | |
| C. | 缆绳与竖直方向的夹角α可能大于角β | |
| D. | 缆绳拉力F1的功率保持不变 |
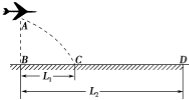 如图所示,在水平地面上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.求:
如图所示,在水平地面上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.求:
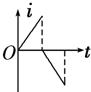
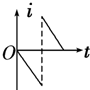
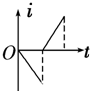
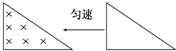 如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )
如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )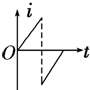
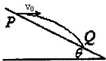 如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上的P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,不考虑其他可能存在的阻力,万有引力常量为G.求该星球的密度和该星球上的第一宇宙速度.
如图所示,宇航员站在某质量分布均匀的星球表面一斜坡上的P点,沿水平方向以初速度v0抛出一个小球,测得小球经时间t落到斜坡上另一点Q,斜面的倾角为θ,已知该星球半径为R,不考虑其他可能存在的阻力,万有引力常量为G.求该星球的密度和该星球上的第一宇宙速度.