题目内容
11．
如图所示，x轴在水平地面上，y轴竖直向上，在y轴上的P点分别沿x轴正方向和y轴正方向以相同大小的初速度抛出两个小球a和b，不计空气阻力，若b上行的最大高度等于P点离地的高度，则从抛出到落地，有（ ）| A． | a的运动时间是b的运动时间的$\sqrt{2}$倍 | |
| B． | a的位移大小是b的位移大小的$\sqrt{5}$倍 | |
| C． | a、b落地时的速度相同，因此动能一定相同 | |
| D． | a、b落地时的速度不同，但动能可能相同 |
分析 a做平抛运动，运动平抛运动的规律得出时间与高度的关系．b做竖直上抛运动，上升过程做匀减速运动，下落做自由落体运动，分两段求运动时间，即可求解时间关系；b的位移大小等于抛出时的高度．根据b的最大高度，求出初速度与高度的关系，即可研究位移关系；根据机械能守恒分析落地时动能关系．
解答 解：
A、设P点离地的高度为h．对于b：b做竖直上抛运动，上升过程与下落过程对称，则b上升到最大的时间为t1=$\sqrt{\frac{2h}{g}}$，从最高点到落地的时间为 t2=$\sqrt{\frac{2×2h}{g}}$，故b运动的总时间tb=t1+t2=（$\sqrt{2}$+1）$\sqrt{\frac{2h}{g}}$；
对于a：做平抛运动，运动时间为ta=$\sqrt{\frac{2h}{g}}$；则有tb=（$\sqrt{2}$+1）ta．故A错误．
B、对于b：h=$\frac{{v}_{0}^{2}}{2g}$，则得v0=$\sqrt{2gh}$；对于a：水平位移为x=v0t=$\sqrt{2gh}$•$\sqrt{\frac{2h}{g}}$=2h，a的位移为 xa=$\sqrt{{h}^{2}+（2h）^{2}}$=$\sqrt{5}$h，而b的位移大小为h，则a的位移大小是b的位移大小的$\sqrt{5}$倍．故B正确．
CD、根据机械能守恒定律得：Ek=mgh+$\frac{1}{2}m{v}_{0}^{2}$，若两球的质量相等，则两球落地时动能相同．而速度方向不同，则落地时速度不同．故C错误，D正确．
故选：BD
点评 本题的解题关键要掌握竖直上抛和平抛两种运动的研究方法及其规律，并根据机械能守恒分析落地时动能关系．
练习册系列答案
相关题目
18．
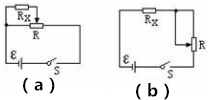用伏安法测电阻，应当用滑动变阻器改变通过待测电阻的电流强度，以便多测几组数据．如图所示，变阻器有a、b两种接法，关于这两种接法，下列说法中正确的是（ ）
用伏安法测电阻，应当用滑动变阻器改变通过待测电阻的电流强度，以便多测几组数据．如图所示，变阻器有a、b两种接法，关于这两种接法，下列说法中正确的是（ ）| A． | 变阻器在a图中作分压器使用，在b图中作限流器使用 | |
| B． | 若变阻器的全阻值比待测电阻小时，用b电路能较大范围地调节Rx中的电流强度 | |
| C． | 若变阻器的全阻值比待测电阻大时，用a电路能较大范围地调节Rx中的电流强度 | |
| D． | 若变阻器的全阻值比待测电阻小得多时，用a电路能较大范围地调节Rx中的电流强度 |
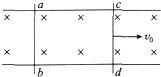如图所示，水平面上有足够长的光滑导轨，匀强磁场B垂直导轨平面，相同的金属棒ab、cd质量均为m，长为L，开始时ab静止，cd初速为v0，则最后ab的速度大小为$\frac{1}{2}{v}_{0}$，整个过程回路中产生的热量为$\frac{1}{4}m{v}_{0}^{2}$．
在如图所示电路，电压表和电流表均为理想电表，固定电阻R=90Ω，R0是可变电阻，可调的最大阻值为400Ω，当开关S断开时，电压表的读数为5V；当开关S闭合，调可变电阻，使电压表的读数为4.7V，电流表的读数为0.03A．
16．
一物体在外力的作用下从静止开始做直线运动，合外力方向不变，大小随时间的变化如图所示，设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2，速度分别是v1和v2，合外力从开始至t0时刻做的功是W1，从t0至2t0时刻做的功是W2，则（ ）
一物体在外力的作用下从静止开始做直线运动，合外力方向不变，大小随时间的变化如图所示，设该物体在t0和2t0时刻相对于出发点的位移分别是x1和x2，速度分别是v1和v2，合外力从开始至t0时刻做的功是W1，从t0至2t0时刻做的功是W2，则（ ）| A． | x2=$\frac{5}{2}$x1 v2=2v1 | B． | x2=$\frac{7}{2}$x1 v2=$\frac{3}{2}$v1 | ||
| C． | x2=$\frac{7}{2}$x1 W2=$\frac{5}{4}$W1 | D． | v2=2v1 W2=$\frac{5}{2}$W1 |
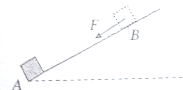如图所示，斜面倾角θ=30°的光滑斜面上，高h=1m的位置B点，放置一质量为m=1kg的物体．（g取10m/s2） 
