题目内容
1.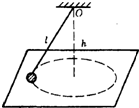 用长L=0.5米的细绳,一端拴一质量m=1千克的小球,另一端固定在离水平桌高h=O.3米的0点上,使小球在光滑桌面上做匀速圆周运动(图).如果运动速率v=1.2米/秒,则此时绳对球的拉力为4.5N,球对桌面的压力为7.3N.为使小球不离开桌面做圆周运动,它的速率不能超过2.3.(g取10m/s2)
用长L=0.5米的细绳,一端拴一质量m=1千克的小球,另一端固定在离水平桌高h=O.3米的0点上,使小球在光滑桌面上做匀速圆周运动(图).如果运动速率v=1.2米/秒,则此时绳对球的拉力为4.5N,球对桌面的压力为7.3N.为使小球不离开桌面做圆周运动,它的速率不能超过2.3.(g取10m/s2)
分析 对小球受力分析,小球受到重力,绳子的拉力以及桌面的支持力;根据拉力和重力的合力提供向心力列式求解即可.
解答 解:当小球的速度比较小时,小球受重力、支持力和拉力,设细绳与竖直方向之间的夹角是θ,运动的半径为r,则:
$r=\sqrt{{L}^{2}-{h}^{2}}=\sqrt{0.{5}^{2}-0.{3}^{2}}=0.4$m
sinθ=$\frac{r}{L}=\frac{0.4}{0.5}=0.8$
cosθ=$\frac{h}{L}=\frac{0.3}{0.5}=0.6$
水平方向:$Fsinθ=\frac{m{v}^{2}}{r}$
代入数据得:F=4.5N
竖直方向:N+Fcosθ=mg
代入数据得:N=7.3N
当物块恰好要离开桌面时,物块受到重力和细绳的拉力的作用,则:
在竖直方向合力为零,在水平方向所需向心力为$\frac{m{v}^{2}}{r}$,得:
F′cosθ=mg
所以:$F′=\frac{50}{3}$N
F′sinθ=$\frac{m{v}^{2}}{r}$
得:$v=\sqrt{\frac{16}{3}}=2.3$m/s
故答案为:4.5,7.3,2.3
点评 本题关键找出临界状态,然后根据牛顿第二定律和向心力公式列式求解,知道当桌面对小球无支持力时,小球将离开桌面,难度适中.

练习册系列答案
相关题目
12.关于位移和路程,下列说法正确的是( )
| A. | 物体沿直线向某一方向运动,通过的路程就是位移 | |
| B. | 物体沿直线向某一方向运动,通过的路程等于位移的大小 | |
| C. | 物体通过一段路程,其位移可能是零 | |
| D. | 物体通过的路程不等,但位移可能相同,反之两物体通过的位移不同时,路程可能相同 |
9.下列说法中正确的是( )
| A. | 只有体积很小的物体才可以当作质点 | |
| B. | “地球围绕太阳转”,是以地球为参考系 | |
| C. | “第3秒初”就是第2秒末,指的是时刻 | |
| D. | 位移的大小和路程总是相等的,但位移是矢量,路程是标量 |
6.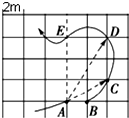 如图所示,物体沿曲线轨迹的箭头方向运动,在AB、ABC、ABCD、ABCDE四段轨迹上运动所用的时间分别是1s、2s、3s、4s,已知方格的边长为2m.下列说法正确的是( )
如图所示,物体沿曲线轨迹的箭头方向运动,在AB、ABC、ABCD、ABCDE四段轨迹上运动所用的时间分别是1s、2s、3s、4s,已知方格的边长为2m.下列说法正确的是( )
 如图所示,物体沿曲线轨迹的箭头方向运动,在AB、ABC、ABCD、ABCDE四段轨迹上运动所用的时间分别是1s、2s、3s、4s,已知方格的边长为2m.下列说法正确的是( )
如图所示,物体沿曲线轨迹的箭头方向运动,在AB、ABC、ABCD、ABCDE四段轨迹上运动所用的时间分别是1s、2s、3s、4s,已知方格的边长为2m.下列说法正确的是( )| A. | 物体在AB段的平均速度为2m/s | |
| B. | 物体在ABC段的平均速度为$\sqrt{5}$m/s | |
| C. | AB段的平均速度比ABC段的平均速度更能反映物体处于A点时的瞬时速度 | |
| D. | 物体在B点的速度等于AC段的平均速度 |
10.甲、乙两个质点同时、同地向同一方向做直线运动,它们的v-t图象如图所示,则由图象可知( )

| A. | 乙物体的加速度为5 m/s2 | |
| B. | 在2s末时乙追上甲 | |
| C. | t=6s时,甲、乙相距20m | |
| D. | 在连续相等的时间内,乙通过的位移之比为:1:3:5:… |

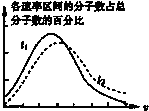 如图所示是一定质量的氧气在不同的温度下,分子的速率分布情况,实线和虚线分别对应的温度为t1和t2,则由图可得t1<t2(选填“<”、“<”或“=”);曲线反映的分子速率分布规律是中间多,两头小.
如图所示是一定质量的氧气在不同的温度下,分子的速率分布情况,实线和虚线分别对应的温度为t1和t2,则由图可得t1<t2(选填“<”、“<”或“=”);曲线反映的分子速率分布规律是中间多,两头小.