题目内容
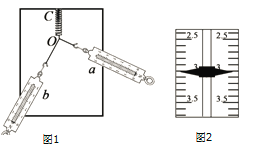
【题目】如图所示，a、b为竖直正对放置的平行金属板构成的偏转电场，其中a板带正电，两板间的电压为U，在金属板下方存在一有界的匀强磁场，磁场的上边界为与两金属板下端重合的水平面PQ，PQ下方的磁场范围足够大，磁场的磁感应强度大小为B，一带正电粒子以速度v0从两板中间位置与a、b平行方向射入偏转电场，不计粒子重力，粒子通过偏转电场后从PQ边界上的M点进入磁场，运动一段时间后又从PQ边界上的N点射出磁场，设M、N两点距离为x（M、N点图中未画出），从N点射出的速度为v，则以下说法中正确的是
A. 只增大带电粒子的比荷大小，则v减小
B. 只增大偏转电场的电压U的大小，则v减小
C. 只减小初速度v0的大小，则x不变
D. 只减小偏转电场的电压U的大小，则x不变
【答案】D
【解析】粒子在电场中，水平方向
；竖直方向
， 
； 
，解得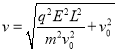
，则只增大带电粒子的比荷大小，则v增大，选项A错误；只增大偏转电场的电压U的大小，则E变大，v变大，选项B错误；减小初速度v0的大小，则导致进入磁场的速度减小，由半径公式R=
，可知，导致半径减小，则x也减小，故C错误；减小偏转电场的电压U的大小，设速度与磁场边界的夹角为θ，则由半径公式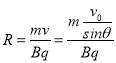
，结合几何关系，可得：x=2Rsinθ=
，则会导致x不变，故D正确；故选D．
练习册系列答案
相关题目
