题目内容
 (2008?东城区三模)如图所示,水平轨道AB与放置在竖直平面内的1/4圆弧轨道BC相连,圆弧轨道的B端的切线沿水平方向.一质量m=1.0kg的滑块(可视为质点),在水平恒力F=5.0N的作用下,从A点由静止开始运动,已知A、B之间的距离s=5.5m,滑块与水平轨道间的动摩擦因数μ=0.10,圆弧轨道的半径R=0.30m,取g=10m/s2.
(2008?东城区三模)如图所示,水平轨道AB与放置在竖直平面内的1/4圆弧轨道BC相连,圆弧轨道的B端的切线沿水平方向.一质量m=1.0kg的滑块(可视为质点),在水平恒力F=5.0N的作用下,从A点由静止开始运动,已知A、B之间的距离s=5.5m,滑块与水平轨道间的动摩擦因数μ=0.10,圆弧轨道的半径R=0.30m,取g=10m/s2.(1)求当滑块运动的位移为2.0m时的速度大小;
(2)当滑块运动的位移为2.0m 时撤去F,求滑块通过B点时对圆弧轨道的压力大小;
(3)滑块运动的位移为2.0m时撤去F后,若滑块恰好能上升到圆弧轨道的最高点,求在圆弧轨道上滑块克服摩擦力所做的功.
分析:(1)滑块在水平地面上做匀加速直线运动,由牛顿第二定律可得出加速度,由运动学公式可求得2.0m时的速度;
(2)对2m位置到B过程运用牛顿第二定律求解加速度,再结合速度位移关系公式求解B点的速度,在B点,重力和支持力的合力提供向心力,根据牛顿第二定律列式求解支持力,结合牛顿第三定律得到压力;
(3)撤去拉力后,滑块做减速运动,由牛顿第二定律及运动学公式可解得滑块到达B点时的速度;对B到C过程由动能定理可求向滑块克服摩擦力所做的功.
(2)对2m位置到B过程运用牛顿第二定律求解加速度,再结合速度位移关系公式求解B点的速度,在B点,重力和支持力的合力提供向心力,根据牛顿第二定律列式求解支持力,结合牛顿第三定律得到压力;
(3)撤去拉力后,滑块做减速运动,由牛顿第二定律及运动学公式可解得滑块到达B点时的速度;对B到C过程由动能定理可求向滑块克服摩擦力所做的功.
解答:解:(1)设滑块的加速度为a1,根据牛顿第二定律
F-μmg=ma1
解得:a1=4.0m/s2
设滑块运动的位移为2.0m时的速度大小为v,根据运动学公式
v2=2a1s1
解得:v=4.0m/s
(2)设撤去拉力F后的加速度为a2,根据牛顿第二定律
μmg=ma2
解得:a2=μg=1.0m/s2
设滑块通过B点时的速度大小为vB,根据运动学公式
-v2=-2a2(S-S1)
解得:vB=3.0m/s
设滑块在B点受到的支持力为NB,根据牛顿第二定律
NB-mg=m
解得:NB=40N
根据牛顿第三定律,滑块通过B点时对圆弧轨道的压力为40N.
(3)设圆弧轨道的摩擦力对滑块做功为W,根据动能定理
-mgR+W=0-
m
解得:W=-1.5J
圆弧轨道上滑块克服摩擦力所做的功为1.5J.
答:(1)求当滑块运动的位移为2.0m时的速度大小为4.0m/s;
(2)当滑块运动的位移为2.0m 时撤去F,滑块通过B点时对圆弧轨道的压力大小为40N;
(3)滑块运动的位移为2.0m时撤去F后,若滑块恰好能上升到圆弧轨道的最高点,在圆弧轨道上滑块克服摩擦力所做的功为1.5J.
F-μmg=ma1
解得:a1=4.0m/s2
设滑块运动的位移为2.0m时的速度大小为v,根据运动学公式
v2=2a1s1
解得:v=4.0m/s
(2)设撤去拉力F后的加速度为a2,根据牛顿第二定律
μmg=ma2
解得:a2=μg=1.0m/s2
设滑块通过B点时的速度大小为vB,根据运动学公式
| v | 2 B |
解得:vB=3.0m/s
设滑块在B点受到的支持力为NB,根据牛顿第二定律
NB-mg=m
| ||
| R |
解得:NB=40N
根据牛顿第三定律,滑块通过B点时对圆弧轨道的压力为40N.
(3)设圆弧轨道的摩擦力对滑块做功为W,根据动能定理
-mgR+W=0-
| 1 |
| 2 |
| v | 2 B |
解得:W=-1.5J
圆弧轨道上滑块克服摩擦力所做的功为1.5J.
答:(1)求当滑块运动的位移为2.0m时的速度大小为4.0m/s;
(2)当滑块运动的位移为2.0m 时撤去F,滑块通过B点时对圆弧轨道的压力大小为40N;
(3)滑块运动的位移为2.0m时撤去F后,若滑块恰好能上升到圆弧轨道的最高点,在圆弧轨道上滑块克服摩擦力所做的功为1.5J.
点评:多过程的运动学题目如果不涉及时间,一般都可以用动能定理列式求解,如本题中前2m及全程都可以应用动能定理求解,步骤将更为简洁.

练习册系列答案
相关题目
(2008?东城区三模)某研究性学习小组在探究光的折射过程中,研究折射角与入射角之间的关系,当光由空气斜射入玻璃中时,测得实验数据如下表
|
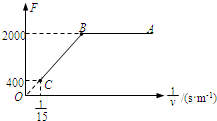 (2008?东城区三模)“绿色奥运”是2008年北京奥运会的三大理念之一,奥组委决定在各比赛场馆使用新型节能环保电动车,届时奥运会500名志愿者将担任司机,负责接送比赛选手和运输器材.在检测某款电动车性能的某次实验中,质量为800kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出
(2008?东城区三模)“绿色奥运”是2008年北京奥运会的三大理念之一,奥组委决定在各比赛场馆使用新型节能环保电动车,届时奥运会500名志愿者将担任司机,负责接送比赛选手和运输器材.在检测某款电动车性能的某次实验中,质量为800kg的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出 (2008?东城区三模)某中学物理实验小组利用DIS系统(数字化信息实验室系统),观察超重和失重现象.他们在学校电梯内做实验.在电梯天花板上固定一个力传感 器,测量时挂钩向下.并在钩上悬挂一个重为10N的钩码,在电梯运动过程中,计算机显示屏上显示出如图所示图线.根据图线分析可知,下列说法中正确的是( )
(2008?东城区三模)某中学物理实验小组利用DIS系统(数字化信息实验室系统),观察超重和失重现象.他们在学校电梯内做实验.在电梯天花板上固定一个力传感 器,测量时挂钩向下.并在钩上悬挂一个重为10N的钩码,在电梯运动过程中,计算机显示屏上显示出如图所示图线.根据图线分析可知,下列说法中正确的是( )