题目内容
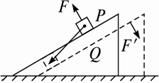
如图
图
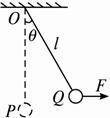
(1)质点由半径a到b所需的时间.
(2)质点在半径为b的圆周上运动的角速度.
解析:(1)质点在半径为a的圆周上以角速度ω1做匀速圆周运动,其线速度为va=ω![]() ,则质点由半径a到b所需的时间为:
,则质点由半径a到b所需的时间为: ![]() .
.

图
(2)当绳子刚被拉直时,球的速度为va=ω
则质点沿半径为b的圆周做匀速圆周运动的角速度为![]() .
.
答案:(1)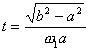 (2)
(2)![]()

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目