题目内容
9.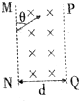 如图所示,MN、PQ为匀强磁场的边界,且MN平行于PQ,已知匀强磁场磁感应强度B=0.1T,方向垂直于纸面向内,磁场宽度d=0.3m,有一带负电的粒子,m=2×10-26kg,q=-1.6×10-18C,当粒子从MN边界以θ=60°的初速度垂直于磁场方向进入磁场,要使粒子不从PQ边界射出,则粒子的速度大小应是多少?(不计粒子所受重力)
如图所示,MN、PQ为匀强磁场的边界,且MN平行于PQ,已知匀强磁场磁感应强度B=0.1T,方向垂直于纸面向内,磁场宽度d=0.3m,有一带负电的粒子,m=2×10-26kg,q=-1.6×10-18C,当粒子从MN边界以θ=60°的初速度垂直于磁场方向进入磁场,要使粒子不从PQ边界射出,则粒子的速度大小应是多少?(不计粒子所受重力)
分析 根据题意确定运动轨迹,再由圆心角与周期公式,即可确定最长运动的时间;根据半径公式与半径的取值,即可求解
解答 解:如右图,由题意知,要使离子不射出PQ边界,离子轨迹的圆心角为120度,所以半径R=$\frac{2}{3}d$=0.2m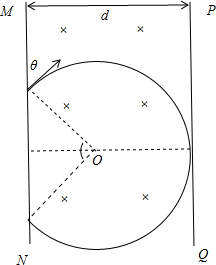
洛伦兹力提供向心力:qvB=m$\frac{{v}^{2}}{R}$
解得v=$\frac{qBR}{m}$=$\frac{1.6×1{0}^{-18}×0.1×0.2}{2×1{0}^{-26}}$=1.6×106m/s
答:粒子的速度大小应是1.6×106m/s
点评 考查牛顿第二定律的应用,掌握几何关系在题中的运用,理解在磁场中运动时间与圆心角的关系.注意本题关键是画出正确的运动轨迹

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
19. 如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )
如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )
 如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )
如图所示,甲分子固定在坐标原点O,只在两分子间的作用力作用下,乙分子沿x轴方向运动,两分子间的分子势能Eρ与两分子间距离x的变化关系如图中曲线所示,设分子动能和势能之和为0,则( )| A. | 乙分子在P点(x=x2)时加速度最大 | B. | 乙分子在P点(x=x2)时动能最大 | ||
| C. | 乙分子在Q点(x=x1)时处于平衡状态 | D. | 乙分子在Q点(x=x1)时分子势能最小 |
20.关于楞次定律,下列说法正确的是( )
| A. | 感应电流的磁场总是要阻碍引起感应电流的磁通量的变化 | |
| B. | 闭合电路的一部分导体在磁场中运动时,必受磁场阻碍作用 | |
| C. | 原磁场穿过闭合回路的磁通量磁增加时,感应电流的磁场与原磁场同向 | |
| D. | 感应电流的磁场总是跟原磁场反向,阻碍原磁场的变化 |
17.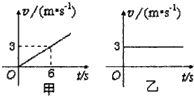 一快艇从离岸边100m远的河中由静止向岸边行驶,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )
一快艇从离岸边100m远的河中由静止向岸边行驶,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )
 一快艇从离岸边100m远的河中由静止向岸边行驶,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )
一快艇从离岸边100m远的河中由静止向岸边行驶,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )| A. | 快艇的运动轨迹一定为直线 | |
| B. | 快艇的运动轨迹可能为曲线,也可能为直线 | |
| C. | 快艇最快到达岸边所用的时间为10s | |
| D. | 快艇最快到达岸边所用的时间为20s |
14. 图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图所示.现将S1接1、S2闭合,此时L2正常发光.下列说法正确的是( )
图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图所示.现将S1接1、S2闭合,此时L2正常发光.下列说法正确的是( )
 图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图所示.现将S1接1、S2闭合,此时L2正常发光.下列说法正确的是( )
图甲中理想变压器原、副线圈的匝数之比n1:n2=5:1,电阻R=20Ω,L1、L2为规格相同的两只小灯泡,S1为单刀双掷开关.原线圈接正弦交变电源,输入电压u随时间t的变化关系如图所示.现将S1接1、S2闭合,此时L2正常发光.下列说法正确的是( )| A. | 输入电压u的表达式u=20$\sqrt{2}$sin(50π)V | |
| B. | 只断开S2后,L1、L2均正常发光 | |
| C. | 若S1换接到2后,R消耗的电功率为2W | |
| D. | 只断开S2后,原线圈的输入功率减小 |
18.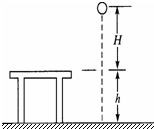 如图所示,桌面离地高度为h=1m,质量为1kg的小球,从离桌面H=2m高处由静止下落.若以桌面为参考平面,则小球落地时的重力势能及整个过程中小球重力做功分别为 (g=10m/s2)( )
如图所示,桌面离地高度为h=1m,质量为1kg的小球,从离桌面H=2m高处由静止下落.若以桌面为参考平面,则小球落地时的重力势能及整个过程中小球重力做功分别为 (g=10m/s2)( )
 如图所示,桌面离地高度为h=1m,质量为1kg的小球,从离桌面H=2m高处由静止下落.若以桌面为参考平面,则小球落地时的重力势能及整个过程中小球重力做功分别为 (g=10m/s2)( )
如图所示,桌面离地高度为h=1m,质量为1kg的小球,从离桌面H=2m高处由静止下落.若以桌面为参考平面,则小球落地时的重力势能及整个过程中小球重力做功分别为 (g=10m/s2)( )| A. | -10J,10J | B. | 10J,10J | C. | -10J,30J | D. | 10J,30J |
19.如图所示,下列说法正确的是( )
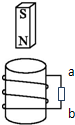

| A. | 只要有磁铁就一定有电流 | |
| B. | 若磁铁向上运动,则a、b两点电势高低是φa<φb | |
| C. | 若磁铁向下运动,则电阻中电流的方向时从b到a | |
| D. | 若磁铁向下运动,则a、b两点电势高低是φa>φb |
 如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处飞出,最后落在水平面上,已知小球落地点C距B处的水平距离为4R.求小球对轨道口B处的压力为多大?
如图所示,一光滑的半径为R的半圆形轨道放在水平面上,一个质量为m的小球以某一速度冲上轨道,然后小球从轨道口B处飞出,最后落在水平面上,已知小球落地点C距B处的水平距离为4R.求小球对轨道口B处的压力为多大?