题目内容
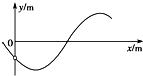 在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+2π/3)m,式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5m/s的初速度沿杆向下运动,取重力加速度g=10m/s2.求:
在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为y=2.5cos(kx+2π/3)m,式中k=1m-1.将一光滑小环套在该金属杆上,并从x=0处以v0=5m/s的初速度沿杆向下运动,取重力加速度g=10m/s2.求:(1)当小环运动到x=π/3m时的速度多大?
(2)该小环在x轴方向最远能运动到多远处.
分析:本题(1)的关键是根据曲线方程求出小环在x=0和x=
时对应的纵坐标值,然后根据动能定理即可求解;题(2)的关键是明确小环运动到最远的含义是末速度等于0时,根据动能定理可求出此过程发生的位移h,然后根据h=
求出
,代入曲线方程即可求出x.
| π |
| 3 |
| y | 1 |
| -y | 2 |
| y |
解答:解:(1)当x=0时,
=2.5cos
π=-1.25m,当x=
时,
=2.5cosπ=-2.5m,由此可知,小环下落的高度为△y=
=-1.25m-2.5m=1.25m,由动能定理得:
mg△y=
m
-
,代入数值得:v=5
m/s.
(2)当小环速度为零时,设上升的高度为h,由动能定理得:-mgh=0-
m
,解得h=
=1.25m,即
=h=1.25,解得
=0,即当y=0时小环速度为零,所以有2.5cos(kx+
π)=0,解得x=
m.
答:(1)当小环运动到x=
m时的速度为5
m/s.
(2)该小环在x轴方向最远能运动到
m远处.
| y | 1 |
| 2 |
| 3 |
| π |
| 3 |
| y | 2 |
| y | 1 |
| -y | 2 |
mg△y=
| 1 |
| 2 |
| v | 2 |
| 1 |
| 2 |
| mv | 2 0 |
| 2 |
(2)当小环速度为零时,设上升的高度为h,由动能定理得:-mgh=0-
| 1 |
| 2 |
| v | 2 0 |
| ||
| 2g |
| y | 1 |
| -y | 2 |
| y | 2 |
| 2 |
| 3 |
| 5π |
| 6 |
答:(1)当小环运动到x=
| π |
| 3 |
| 2 |
(2)该小环在x轴方向最远能运动到
| 5π |
| 6 |
点评:明确曲线方程与位移方程的区别,对做曲线运动的物体应用动能定理求解速度的大小.

练习册系列答案
相关题目

 如图,两根长度分别为L1和L2的光滑杆AB和BC在B点垂直焊接,当按图示方式固定在竖直平面内时,将一滑环从B点由静止释放,分别沿BA和BC滑到杆的底端经历的时间相同,则这段时间为( )
如图,两根长度分别为L1和L2的光滑杆AB和BC在B点垂直焊接,当按图示方式固定在竖直平面内时,将一滑环从B点由静止释放,分别沿BA和BC滑到杆的底端经历的时间相同,则这段时间为( ) B.
B.
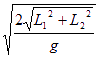 D.
D.