题目内容
【题目】如图所示，oa、ob是竖直平面内两根固定的光滑细杆，o、a、b、c位于同一圆周上，c为圆周的最高点，a为最低点，ob经过圆心．每根杆上都套着一个小滑环，两个滑环都从o点无初速释放，用t1、t2分别表示滑环到达a、b所用的时间，则下列关系正确的是（ ）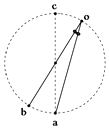
A.t1＞t2
B.t1＜t2
C.t1=t2
D.无法确定
【答案】B
【解析】解：以O点为最高点，取合适的竖直直径oa作等时圆，交ob于c，如图所示，显然o到a、c才是等时的，比较图示位移ob＞oc，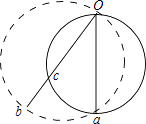
故推得t1＜t2 ， 故B正确
故选：B．
【考点精析】解答此题的关键在于理解匀变速直线运动的速度、位移、时间的关系的相关知识，掌握速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值．
练习册系列答案
智能训练练测考系列答案
相关题目
