��Ŀ����
18����ͼ��ʾ����xOy����ϵ�У�y������Ŀռ����з�Χ������ǿ�ų�����Ÿ�Ӧǿ��ΪB������ֱֽ�����y����Ҳ������ˮƽ�����30���б�����Ϸ�����ǿ�糡������Ϊm������Ϊq�Ĵ��������Ӧ���x�������ϵ�P�����ٶ�v��x�Ḻ���᷽���60��������ǿ�ų�������y���ϵ�Q�㣨ͼ��Ϊ�����������ŵ糡�߷�������Ҳ����ǿ�糡��������������ͬ�Ĵ���������b��P����ijһ�ٶ���x���������60��������ǿ�ų�����y���ֱ�ڵ糡���������ұߵ���ǿ�糡�У����������Ӽ�Ŀ������������ӵ���������
��1��P�㵽O��ľ��룻
��2����������b�ij��ٶȣ�
��3��Ҫʹ������������Q�������������Ӵ�P�������ʱ��֮��Ϊ��t��
���� ��1���������������ṩ�����������a�����ڴų����˶�Բ���˶��İ뾶�����ɼ��ι�ϵ��P��O��ľ��룮
��2������b���ӵ��˶��켣���ɼ���֪ʶ�����켣�뾶��������ţ�ٵڶ�����������ٶȣ�
��3���ȸ��ݹ켣��Բ�Ľ�������������ڴų��е��˶�ʱ�䣮b���ӽ���糡������ƽ���˶���a���ȼ���ֱ���˶���������ƽ���˶����ȼ���ֱ���˶���λ�ƹ�ʽ��λ����ʽ��������ڵ糡�е��˶�ʱ�䣬�������ʱ��
��� 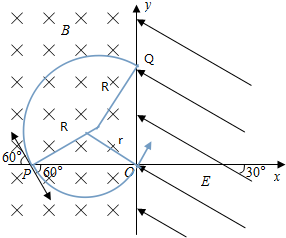 �⣺��1������a���ӣ��������������ṩ����������
�⣺��1������a���ӣ��������������ṩ����������
qvB=m$\frac{{v}^{2}}{R}$���� R=$\frac{mv}{qB}$
����a���ӵ��˶��켣����ͼ���ɼ���֪ʶ�ɵ� $\overline{PO}$=Rcos30��+Rsin30��=$\frac{\sqrt{3}+1}{2}$R=$\frac{��\sqrt{3}+1��mv}{2qB}$
��2�������֪b��������糡ʱ�ٶ���x��������ļн�Ϊ60�㣬��֪b���Ӵ�O������糡������b���ӵ��˶��켣���ɼ���֪ʶ�ã�
2rcos30��=$\overline{PO}$
�ɵ� r=$\frac{\sqrt{3}+3}{6}$R=$\frac{��\sqrt{3}+3��mv}{6qB}$
��b���ӵij��ٶ�Ϊv�䣬��r=$\frac{mv��}{qB}$�� v��=$\frac{\sqrt{3}+3}{6}$v
��3��a�����ڴų����˶�ʱ��Ϊ ta=$\frac{150��}{360��}$T=$\frac{5}{12}$T��T=$\frac{2��m}{qB}$
b�����ڴų����˶�ʱ��Ϊ tb=$\frac{120��}{360��}$T=$\frac{1}{3}$T��
Q��O��ľ���Ϊ $\overline{QO}$=Rcos30��+Rsin30��=$\frac{\sqrt{3}+1}{2}$R
b�����ڵ糡������ƽ���˶�����
��ֱ�ڵ糡�߷����� $\overline{QO}$cos30��=v��tb��
������ tb��=$\frac{3R}{2v}$=$\frac{3��\sqrt{3}+1��m}{4qB}$
�������Ӵ�P�������ʱ��֮��Ϊ��t=tb+tb��-ta=$\frac{3+3\sqrt{3}+��}{4}$$•\frac{m}{qB}$
��
��1��P�㵽O��ľ���Ϊ$\frac{��\sqrt{3}+1��mv}{2qB}$��
��2����������b�ij��ٶ�Ϊ$\frac{\sqrt{3}+3}{6}$v��
��3��Ҫʹ������������Q�������������Ӵ�P�������ʱ��֮��Ϊ��tΪ$\frac{3+3\sqrt{3}+��}{4}$$•\frac{m}{qB}$��
���� ���⿼����������ڳ��������˶�ģ�ͣ�����Բ���˶�����ƽ���˶��������ۺϷ����������Լ��ռ����������������ʱһ�߷���һ�����˶��켣�������˶��켣������ȷ��ã�

 ��ͼ���ڵ���Q�����ĵ糡�У����������������̽���q1��q2�ֱ�����A��B���㣬����Ϊ�����ߣ�ȡ����Զ������Ϊ�㣬����q1��q2�ƶ���C��Ĺ����е糡������������ȣ�������˵����ȷ���ǣ�������
��ͼ���ڵ���Q�����ĵ糡�У����������������̽���q1��q2�ֱ�����A��B���㣬����Ϊ�����ߣ�ȡ����Զ������Ϊ�㣬����q1��q2�ƶ���C��Ĺ����е糡������������ȣ�������˵����ȷ���ǣ�������| A�� | A����Ƶ���B����� | |
| B�� | A��B����ĵ糡ǿ����� | |
| C�� | q1�ĵ����С��q2�ĵ���� | |
| D�� | q1��C��ĵ����ܴ���q2��C��ĵ����� |
| A�� | m=$\frac{��{v}_{2}-{v}_{0}��M}{{v}_{1}+{v}_{2}}$ | B�� | m=$\frac{M{v}_{2}}{{v}_{1}+{v}_{2}}$ | ||
| C�� | m=$\frac{��{v}_{2}-{v}_{0}��M}{{v}_{1}}$ | D�� | m=$\frac{��{v}_{2}-{v}_{0}��M}{{v}_{2}-{v}_{1}}$ |
| A�� | ���IJʺ��������ɫɢ���� | |
| B�� | ȫϢ��Ƭ�����������˹��ƫ������ | |
| C�� | ������˫�����ʵ���У��������������ɺ���Ϊ�Ϲ⣬�����Ƽ��һ����С | |
| D�� | ��Ҷ�ϵ�ˮ���������¾�Ө����ȫ����Ľ�� | |
| E�� | �г�����һ��̫��������װ��Ƭʱ��������Ӧ����ˮƽ���� | |
| F�� | �������������ȫ���˹���ֱ�ߴ����Ľ��� |
 ��ͼ��ʾ��һ����Ϊm��С�����ڹ⻬��ֱ���ϣ����ʵ���һ�˹̶���O�㣬��һ�����С���������ֽ�С���A���ɾ�ֹ�ͷţ�����ֱ���˶���B�㣬��֪OA����С��OB���ȣ����ɴ���OA��OB��λ��ʱ������С��ȣ���С����A��B�Ĺ����У�������
��ͼ��ʾ��һ����Ϊm��С�����ڹ⻬��ֱ���ϣ����ʵ���һ�˹̶���O�㣬��һ�����С���������ֽ�С���A���ɾ�ֹ�ͷţ�����ֱ���˶���B�㣬��֪OA����С��OB���ȣ����ɴ���OA��OB��λ��ʱ������С��ȣ���С����A��B�Ĺ����У�������| A�� | С���ɺ͵��ɵ�ϵͳ��е���غ� | |
| B�� | ���ɵĵ�����С�ȱ�С���� | |
| C�� | ���ٶȵ����������ٶ�g��λ�������� | |
| D�� | ������С�����Ĺ�����С��˷����ɵ������Ĺ� |
 ��ͼ��ʾ��abcΪһȫ�����⾵�����������ǵ���ֱ�������Σ�һ�����̹�ͺ����ɵĸ�ɫ���ͬһλ�ô�ֱ���䵽ac���ϣ��̹�ͺ����ab���Ͼ�������ȫ���䣮�����������O��λ�ò��䣬�ı���ߵ����䷽��������bc��Ĺ���������գ�������
��ͼ��ʾ��abcΪһȫ�����⾵�����������ǵ���ֱ�������Σ�һ�����̹�ͺ����ɵĸ�ɫ���ͬһλ�ô�ֱ���䵽ac���ϣ��̹�ͺ����ab���Ͼ�������ȫ���䣮�����������O��λ�ò��䣬�ı���ߵ����䷽��������bc��Ĺ���������գ�������| A�� | ʹ������߰�ͼ����ʾ����ʱ�뷽��ƫת����⽫�������ab�� | |
| B�� | ʹ������߰�ͼ����ʾ����ʱ�뷽��ƫת���̹⽫�������ab�� | |
| C�� | ʹ������߰�ͼ����ʾ��˳ʱ�뷽��ƫת������ɫ�����ab�棬���⽫������� | |
| D�� | ʹ������߰�ͼ����ʾ��˳ʱ�뷽��ƫת������ɫ�����ab�棬���̹⽫������� |
| A�� | ��������������з������˶��Ķ��ܺͷ���֮������֮�� | |
| B�� | һ�����ڼ��������Ĺ����У��ڲ�����������˶��Ķ���һ������ | |
| C�� | Һ���Ĺ�ѧ���ʲ������ӵ糡�ı仯���仯 | |
| D�� | һ���������壬��ѹǿ����ʱ������ÿ������ڵ�λ���ƽ����ײ���������¶����߶���С | |
| E�� | һ���������壬���¶Ȳ���ʱ������ÿ������ڵ�λ���ƽ����ײ��������������Ӷ���С |
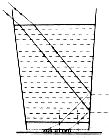 �������Ϸ�һöӲ�ң�ȡһֻ������������ʢ��ˮ��Ȼ��Ѳ�����ѹ��Ӳ���ϣ���ͼ��ʾ���ӱ��ӵIJ��濴ȥ��Ӳ�Ҳ����ˣ����Ǵӱ�����������Ӳ�һ��úõط����������������պ��һЩˮ���ٴӲ����ȥ����ᷢ����ʲô��ͬ������ʹ�����
�������Ϸ�һöӲ�ң�ȡһֻ������������ʢ��ˮ��Ȼ��Ѳ�����ѹ��Ӳ���ϣ���ͼ��ʾ���ӱ��ӵIJ��濴ȥ��Ӳ�Ҳ����ˣ����Ǵӱ�����������Ӳ�һ��úõط����������������պ��һЩˮ���ٴӲ����ȥ����ᷢ����ʲô��ͬ������ʹ�����