题目内容
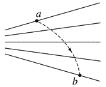
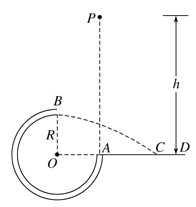
【题目】如图所示,竖直平面内的![]() 圆弧形光滑管道半径R=0.2m,A端与圆心O等高,AD为水平面,B点为管道的最高点且在O的正上方。一个可视为质点的小球质量m=0.4kg,在A点正上方高h=0.6m处的P点由静止释放,自由下落至A点进入管道并通过B点,小球最后落到AD面上的C点处。不计空气阻力,g取10m/s2。求:
圆弧形光滑管道半径R=0.2m,A端与圆心O等高,AD为水平面,B点为管道的最高点且在O的正上方。一个可视为质点的小球质量m=0.4kg,在A点正上方高h=0.6m处的P点由静止释放,自由下落至A点进入管道并通过B点,小球最后落到AD面上的C点处。不计空气阻力,g取10m/s2。求:
(1)小球过A点时的速度vA的大小;
(2)小球过B点时对管壁的压力的大小和方向;
(3)落点C到A点的距离。
【答案】(1)![]() ;(2)12N,竖直向上;(3)
;(2)12N,竖直向上;(3)![]() m
m
【解析】
(1)对小球,根据自由落体运动可得
![]()
代入数据解得
![]() m/s
m/s
(2)小球从P点到B点,只有重力做功,由动能定理得
![]()
代入数据解得
![]()
在B点时,设管壁对其支持力为F,方向竖直向下,由向心力公式得
![]()
解得
![]()
根据牛顿第三定律可知,小球过B点时对管壁的压力的大小为12N,方向竖直向上
(3)从B到C的过程中,由平抛运动规律可得
竖直分运动有
![]()
水平分运动有
![]()
联立解得
![]() m
m
则落点C到A点的距离为
![]()
代入数据解得
![]() m
m

 阅读快车系列答案
阅读快车系列答案【题目】如图所示,足够长的光滑平行金属导轨MN、PQ竖直放置,一个磁感应强度B=0.50T的匀强磁场垂直穿过导轨平面,导轨的上端M与P间连接阻值为R=0.30Ω的电阻,导轨宽度L=0.40m。电阻为r=0.20Ω的金属棒ab紧贴在导轨上,导轨电阻不计,现使金属棒ab由静止开始下滑,通过传感器记录金属棒ab下滑的距离,其下滑距离与时间的关系如下表所示。(g=10m/s2)
时 间t(s) | 0 | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 |
下滑距离h(m) | 0 | 0.10 | 0.30 | 0.70 | 1.20 | 1.70 | 2.20 | 2.70 |

求:
(1)在前0.4s的时间内,金属棒ab电动势的平均值;
(2)金属棒ab的质量m;
(3)在前0.7s的时间内,电阻R上产生的热量QR。