题目内容
(2009?湖北模拟)一列车队从同一地点先后开出n辆汽车在平直的公路上排成直线行驶,各车均由静止出发先做加速度为a的匀加速直线运动,达到同一速度v后改做匀速直线运动,欲使n辆车都匀速行驶时彼此距离均为s,则各辆车依次启动的时间间隔为(不计汽车的大小)( )
分析:设某辆车从静止开始做匀加速直线运动经过时间t速度恰好达到v,其前面一辆车运动时间为t+△t,根据两车的位移差为s即可求解.
解答:解:设某辆车从静止开始做匀加速直线运动经过时间t速度恰好达到v,其前面一辆车运动时间为t+△t,
则s1=
at2,
s1+s=
at2+v?△t.
联立上述方程得各辆车依次启动的时间间隔△t=
,故D项正确.
故选D.
则s1=
| 1 |
| 2 |
s1+s=
| 1 |
| 2 |
联立上述方程得各辆车依次启动的时间间隔△t=
| s |
| v |
故选D.
点评:该题主要考查了匀加速直线运动位移时间公式,难度不大,属于基础题.

练习册系列答案
相关题目
 (2009?湖北模拟)如图所示,可视为点电荷的小物块A、B分别带负电和正电,B固定,其正下方的A静止在绝缘斜面上,则A受力个数可能为( )
(2009?湖北模拟)如图所示,可视为点电荷的小物块A、B分别带负电和正电,B固定,其正下方的A静止在绝缘斜面上,则A受力个数可能为( ) (2009?湖北模拟)如图所示,物体A贴在竖直墙面上,在竖直轻弹簧作用下,A、B保持静止.则物体A的受力个数为( )
(2009?湖北模拟)如图所示,物体A贴在竖直墙面上,在竖直轻弹簧作用下,A、B保持静止.则物体A的受力个数为( )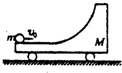 (2009?湖北模拟)右端带有l/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度vo水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )
(2009?湖北模拟)右端带有l/4光滑圆弧轨道质量为M的小车静置于光滑水平面上,如图所示.一质量为m的小球以速度vo水平冲上小车,关于小球此后的运动情况,以下说法正确的是( )