题目内容
18. 如图所示,对均匀细杆的一端施力F,力的方向垂直于杆,要将杆从地板上慢慢地无滑动地抬起,试求杆与地面间的最小摩擦因数.
如图所示,对均匀细杆的一端施力F,力的方向垂直于杆,要将杆从地板上慢慢地无滑动地抬起,试求杆与地面间的最小摩擦因数.
分析 杆处于平衡状态,受力平衡,对杆进行受力分析,画出杆的受力分析图,根据几何关系结合不等式性质求解即可.
解答 解:杆处于一系列可能的动态平衡状态,当杆抬起α角,重力、地面的约束力及F三力汇交,以此为依据作杆三力平衡矢量图:
则tanθ=μ
$\frac{l}{2}cotα=lcot(α+θ)$
整理得:$\frac{1}{μ}=cotθ=2tanα+cotα$
根据不等式基本性质可知,2tanαcotα=2(恒定)
所以当且仅当2tanα=cotα时取等号,$tanα=\frac{\sqrt{2}}{2}$,
所以${μ}_{min}=\frac{\sqrt{2}}{4}$
答:杆与地面间的最小摩擦因数为$\frac{\sqrt{2}}{4}$.
点评 本题是一道动态平衡的问题,关键是正确对物体进行受力分析,找出几何关系并能结合不等式性质求解,是竞赛题,难度较大.

练习册系列答案
相关题目
8.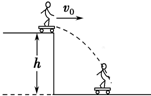 如图,滑板运动员以速度v0从离地高度为h的平台末端水平飞出,落在水平地面上.忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )
如图,滑板运动员以速度v0从离地高度为h的平台末端水平飞出,落在水平地面上.忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )
 如图,滑板运动员以速度v0从离地高度为h的平台末端水平飞出,落在水平地面上.忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )
如图,滑板运动员以速度v0从离地高度为h的平台末端水平飞出,落在水平地面上.忽略空气阻力,运动员和滑板可视为质点,下列表述正确的是( )| A. | v0越大,运动员在空中运动时间越长 | |
| B. | v0越大,运动员落地瞬间速度越大 | |
| C. | 运动员落地瞬间速度与高度h有关 | |
| D. | 运动员落地位置与v0大小无关 |
9.如图甲所示,一个物体放在粗糙的水平地面上.从t=0时刻起,物体在水平向右的力F作用下由静止开始运动.在0到t0时间内物体的加速度a随时间t的变化规律如图乙所示.则( )


| A. | 在0到t0时间内,物体速度逐渐变小 | |
| B. | 在t0时刻,物体速度增加到最大值 | |
| C. | 在0到t0时间内,物体做直线运动 | |
| D. | 在0到t0时间内,物体的速度保持不变 |
7. 如图所示,在半径为R的圆形区域内充满磁感应强度为B的匀强磁场,MN是一竖直放置的感光板.从圆形磁场最高点P以速度v垂直磁场射入大量带正电的粒子,且粒子所带电荷量为q、质量为m.不考虑粒子间的相互作用力及粒子的重力,关于这些粒子的运动,以下说法正确的是( )
如图所示,在半径为R的圆形区域内充满磁感应强度为B的匀强磁场,MN是一竖直放置的感光板.从圆形磁场最高点P以速度v垂直磁场射入大量带正电的粒子,且粒子所带电荷量为q、质量为m.不考虑粒子间的相互作用力及粒子的重力,关于这些粒子的运动,以下说法正确的是( )
 如图所示,在半径为R的圆形区域内充满磁感应强度为B的匀强磁场,MN是一竖直放置的感光板.从圆形磁场最高点P以速度v垂直磁场射入大量带正电的粒子,且粒子所带电荷量为q、质量为m.不考虑粒子间的相互作用力及粒子的重力,关于这些粒子的运动,以下说法正确的是( )
如图所示,在半径为R的圆形区域内充满磁感应强度为B的匀强磁场,MN是一竖直放置的感光板.从圆形磁场最高点P以速度v垂直磁场射入大量带正电的粒子,且粒子所带电荷量为q、质量为m.不考虑粒子间的相互作用力及粒子的重力,关于这些粒子的运动,以下说法正确的是( )| A. | 只要对着圆心入射,出射后均可垂直打在MN上 | |
| B. | 对着圆心入射的粒子,速度越大在磁场中通过的弧长越长,时间也越长 | |
| C. | 即使是对着圆心入射的粒子,其出射方向的反向延长线也不一定过圆心 | |
| D. | 只要速度满足v=$\frac{qBR}{m}$,沿不同方向入射的粒子出射后均可垂直打在MN上 |
5.恒星内部发生着各种热核反应,其中“氦燃烧”的核反应方程为:${\;}_{2}^{4}$He+X→${\;}_{4}^{8}$Be+γ,其中X表示某种粒子,${\;}_{4}^{8}$Be是不稳定的粒子,其半衰期为T,则下列说法正确的是( )
| A. | X 粒子是中子 | |
| B. | 加温或加压可以改变半衰期T的大小 | |
| C. | 经过3个T,剩下的${\;}_{4}^{8}$Be占开始时的$\frac{1}{8}$ | |
| D. | “氦燃烧”的核反应是裂变反应 |

 如图所示,一边长为a的正六边形,六个顶点都放有电荷,试计算六边形中心O点处的场强.
如图所示,一边长为a的正六边形,六个顶点都放有电荷,试计算六边形中心O点处的场强. 长征系列火箭为我国的卫星发射立下了汗马功劳,如图是某监测系统每隔2.5s拍摄的关于起始匀加速阶段火箭的一组照片.已知火箭的长度为40m,用刻度尺测量照片上的长度,结果如图所示.火箭的加速度a=8m/s2,火箭在照片中第2个像所对应时刻的瞬时速度大小v=42 m/s.
长征系列火箭为我国的卫星发射立下了汗马功劳,如图是某监测系统每隔2.5s拍摄的关于起始匀加速阶段火箭的一组照片.已知火箭的长度为40m,用刻度尺测量照片上的长度,结果如图所示.火箭的加速度a=8m/s2,火箭在照片中第2个像所对应时刻的瞬时速度大小v=42 m/s.