题目内容
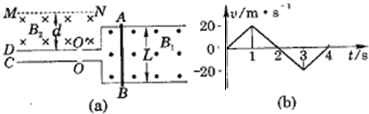
如图(a)所示,两水平放置的平行金属板C、D相距很近,上面分别开有小孔O、O′,水平放置的平行金属导轨与C、D接触良好,且导轨在磁感强度为B1=10T的匀强磁场中,导轨间距L=0.50m,金属棒AB紧贴着导轨沿平行导轨方向在磁场中做往复运动.其速度图象如图(b)所示,若规定向右运动速度方向为正方向,从t=0时刻开始,由C板小孔O处连续不断以垂直于C板方向飘入质量为m=3.2×10-21kg、电量q=1.6×10-19C的带正电的粒子(设飘入速度很小,可视为零).在D板外侧有以MN为边界的匀强磁场B2=10T,MN与D相距d=10cm,B1、B2方向如图所示(粒子重力及其相互作用不计).求:
(1)在0~4.0s时间内哪些时刻发射的粒子能穿过电场并飞出磁场边界MN?
(2)粒子从边界MN射出来的位置之间最大的距离为多少?
(1)在0~4.0s时间内哪些时刻发射的粒子能穿过电场并飞出磁场边界MN?
(2)粒子从边界MN射出来的位置之间最大的距离为多少?

分析:(1)粒子要飞出磁场边界MN,速度最小时,轨迹半径也最小,恰好与MN相切,可得到轨迹半径为d.根据粒子圆周运动的半径r=
求出粒子进入磁场的速度,即为加速获得的末速度,再由动能定理求出加速电压U,由U=ε=B1Lv 求出AB运动的速度,由乙图可求出所求的量.
(2)当AB棒速度最大,产生的感应电动势最大,CD板间电压最大,粒子经加速得到的速度最大,在磁场中轨迹半径也最大,粒子出MN边时,偏转距离最小,根据法拉第定律、动能定理和半径公式结合,并运用几何知识求得粒子从边界MN射出来的位置之间最大的距离.
| mv |
| qB2 |
(2)当AB棒速度最大,产生的感应电动势最大,CD板间电压最大,粒子经加速得到的速度最大,在磁场中轨迹半径也最大,粒子出MN边时,偏转距离最小,根据法拉第定律、动能定理和半径公式结合,并运用几何知识求得粒子从边界MN射出来的位置之间最大的距离.
解答: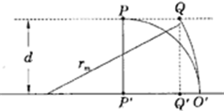 解:(1)由右手定则可判断AB向右运动时,C板电势高于D板电势,粒子被加速进入B2磁场中,AB棒向右运动时产生的电动势E=B1Lv(即为C、D间的电压).粒子经过加速后获得的速度为v′,则有qE=
解:(1)由右手定则可判断AB向右运动时,C板电势高于D板电势,粒子被加速进入B2磁场中,AB棒向右运动时产生的电动势E=B1Lv(即为C、D间的电压).粒子经过加速后获得的速度为v′,则有qE=
mv′2,粒子在磁场B2中做匀速圆周运动,半径r=
.要使粒子恰好穿过,则有r=d.
?联立上述各式代入数据可得 v=5.0m/s.
?故要使粒子能穿过磁场边界MN则要求v>5m/s.
?由速度图象可知,在0.25s<t<1.75s可满足要求.
?(2)当AB棒速度为v=5m/s时,粒子在磁场B2中到达边界MN打在P点上,其轨道半径r=d=0.1m(此时
=r=0.1m)如图所示.
此时粒子向左的位移最大,出射点P与O’的水平距离为d=10cm.
当AB棒速度最大,即v′=20m/s时产生感应电动势为:ε′=B1Lv′=100V
此时带电粒子经加速后速度为v,由动能定理有:q?′=
m
代入数据,解得:v=100m/s
此时带电粒子的轨迹半径为:R′=
=
=0.2m
出射点Q与O’的水平距离为:x=R′-
=0.2-
=0.027m=2.7cm
粒子从边界MN射出来的位置间最大距离为S=d-x═10cm-2.7cm=7.3cm
答:(1)0到4.0s内0.25s<t<1.75s时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN.
(2)粒子从边界MN射出来的位置之间最大的距离为7.3cm
 解:(1)由右手定则可判断AB向右运动时,C板电势高于D板电势,粒子被加速进入B2磁场中,AB棒向右运动时产生的电动势E=B1Lv(即为C、D间的电压).粒子经过加速后获得的速度为v′,则有qE=
解:(1)由右手定则可判断AB向右运动时,C板电势高于D板电势,粒子被加速进入B2磁场中,AB棒向右运动时产生的电动势E=B1Lv(即为C、D间的电压).粒子经过加速后获得的速度为v′,则有qE=| 1 |
| 2 |
| mv′ |
| qB2 |
?联立上述各式代入数据可得 v=5.0m/s.
?故要使粒子能穿过磁场边界MN则要求v>5m/s.
?由速度图象可知,在0.25s<t<1.75s可满足要求.
?(2)当AB棒速度为v=5m/s时,粒子在磁场B2中到达边界MN打在P点上,其轨道半径r=d=0.1m(此时
. |
| O′P′ |
此时粒子向左的位移最大,出射点P与O’的水平距离为d=10cm.
当AB棒速度最大,即v′=20m/s时产生感应电动势为:ε′=B1Lv′=100V
此时带电粒子经加速后速度为v,由动能定理有:q?′=
| 1 |
| 2 |
| v | 2 0 |
代入数据,解得:v=100m/s
此时带电粒子的轨迹半径为:R′=
| mv0 |
| qB2 |
| 3.2×10-21×100 |
| 1.6×10-19×10 |
出射点Q与O’的水平距离为:x=R′-
| R′2-d2 |
| 0.22-0.12 |
粒子从边界MN射出来的位置间最大距离为S=d-x═10cm-2.7cm=7.3cm
答:(1)0到4.0s内0.25s<t<1.75s时刻从O处飘入的粒子能穿过电场并飞出磁场边界MN.
(2)粒子从边界MN射出来的位置之间最大的距离为7.3cm
点评:本题是电磁感应与带电粒子在磁场中运动的综合,要注意挖掘临界条件,掌握电磁学基本知识和基本的分析思路,属于中档题.

练习册系列答案
相关题目
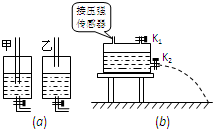
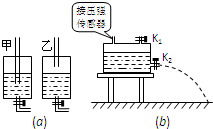
如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水.现在它们顶部各插有一根两端开口的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方.若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是______.(选填“甲”或“乙”)
某同学根据这一现象,猜测水流速度可能与水面上空气的压强有关,他为了验证这一猜想,设计了如图(b)所示的装置,阀门K2控制的容器底部出水小孔是水平的.利用阀门K1可以改变密闭容器内水面上方气体的压强,利用平抛运动知识可获得K2刚打开时流出水的初速度.在一次实验中水深h=1m保持不变的情况下,测出水刚流出时的初速度和对应的水面上气体压强的数据记录如下表所示:
该同学根据表格中数据,推得水面上气体的压强与水流初速度的关系为______,并推出外界大气压强值为______(水的密度ρ=1.0×103kg/m3,重力加速度g=10m/s2).

某同学根据这一现象,猜测水流速度可能与水面上空气的压强有关,他为了验证这一猜想,设计了如图(b)所示的装置,阀门K2控制的容器底部出水小孔是水平的.利用阀门K1可以改变密闭容器内水面上方气体的压强,利用平抛运动知识可获得K2刚打开时流出水的初速度.在一次实验中水深h=1m保持不变的情况下,测出水刚流出时的初速度和对应的水面上气体压强的数据记录如下表所示:
| 压强(×105pa) | 0.98 | 1.08 | 1.22 | 1.40 | 1.62 |
| 初速度(m/s) | 4.01 | 5.99 | 8.00 | 9.99 | 11.99 |

如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水. 现在它们顶部各插有一根两端武器的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方. 若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是 。(选填“甲”或“乙”)
某同学根据这一现象,猜测水流速度可能与水面上空气的压强有关,他为了验证这一猜想,设计了如图(b)所示的装置,阀门K2控制的容器底部出水小孔是水平的。利用阀门K1可以改变密闭容器内水面上方气体的压强,利用平抛运动知识可获得K2刚打开时流出水的初速度。在一次实验中水深h=1m保持不变的情况下,测出水刚流出时的初速度和对应的水面上气体压强的数据记录如下表所示:
| 压强(×105pa) | 0.98 | 1.08 | 1.22 | 1.40 | 1.62 |
| 初速度(m/s) | 4.01 | 5.99 | 8.00 | 9.99 | 11.99 |
该同学根据表格中数据,推得水面上气体的压强与水流初速度的关系为 ,并推出外界大气压强值为 (水的密度ρ=1.0×103kg/m3,重力加速度g=10m/s2).


 如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水.现在它们顶部各插有一根两端开口的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方.若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是
如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水.现在它们顶部各插有一根两端开口的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方.若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是