Question

【题目】如图所示，半径R=1m的光滑半圆轨道AC与高h=8R的粗糙斜面轨道BD放在同一竖直平面内，BD部分水平长度为x=6R．两轨道之间由一条光滑水平轨道相连，水平轨道与斜轨道间有一段圆弧过渡．在水平轨道上，轻质弹簧被a、b两小球挤压（不连接），处于静止状态．同时释放两个小球，a球恰好能通过半圆轨道最高点A，b球恰好能到达斜面轨道最高点B．已知a球质量为m1=2kg，b球质量为m2=1kg，重力力加速度为g=10m/s2 ． （sin37°=0.6，cos37°=0.8）求：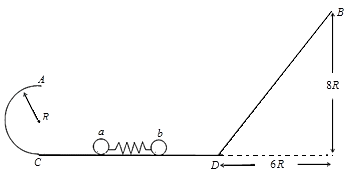

（1）a球经过C点时对轨道的作用力
（2）释放小球前弹簧的弹性势能Ep
（3）小球与斜面间动摩擦因素μ

Answer 1

【答案】
（1）解：以a球为研究对象，恰好通过最高点时，有 m1g=m1

得 vA= = m/s= m/s

a球从C到A的过程，由机械能守恒定律得： m1vC2﹣ m1vA2=m1g2R

C点时受力分析，由牛顿第二定律得：FC﹣m1g=m1

解得：FC=6m1g=120N

由牛顿第三定律知，a球经过C点时对轨道的作用力大小为120N，方向竖直向下．

答：a球经过C点时对轨道的作用力为120N；

（2）解：水平面光滑，弹簧释放两球的过程，a、b及弹簧组成的系统动量守恒，取水平向左为正方向，由动量守恒定律得：

m1vc﹣m2vD=0

解得：vD=10 m/s

释放小球前弹簧的弹性势能为 Ep= m1vC2+ m2vD2=150J

答：释放小球前弹簧的弹性势能Ep为150J；

（3）解：b球从D点恰好到达最高点B过程中，由动能定理：

0﹣ m2vD2=﹣m2g8R﹣μm2gcosθLBD

其中 LBD=10R

解得：μ=

答：小球与斜面间动摩擦因素μ为 ．

【解析】（1）此题的物理过程非常复杂首先对物理过程进行分析，小球恰好过最高点重力提供向心力再结合机械能守恒定律以及合外力提供向心力综合列式求解。
（2）弹簧释放两球的过程中动量守恒根据动量守恒定律和机械能守恒，直接列式求解。
（3）小球到达最高点的过程中根据动能定理列式求解。