题目内容
15.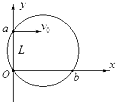 如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L).一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度的方向与x轴正方向的夹角为60°.下列说法正确的是( )
如图所示,在平面直角坐标系中有一个垂直纸面向里的圆形匀强磁场,其边界过原点O和y轴上的点a(0,L).一质量为m、电荷量为e的电子从a点以初速度v0平行于x轴正方向射入磁场,并从x轴上的b点射出磁场,此时速度的方向与x轴正方向的夹角为60°.下列说法正确的是( )| A. | 电子在磁场中运动的半径为L | |
| B. | 电子在磁场中运动的时间为$\frac{2πL}{3{v}_{0}}$ | |
| C. | 磁场的磁感应强度B=$\frac{m{v}_{0}}{2eL}$ | |
| D. | 电子在磁场中做圆周运动的速度不变 |
分析 带电粒子在匀强磁场中在洛伦兹力作用下,做匀速圆周运动.所以由几何关系可确定运动圆弧的半径与已知长度的关系,从而确定圆磁场的圆心,并能算出粒子在磁场中运动时间.
解答 解:A、电子的轨迹半径为R,由几何知识有:Rsin30°=R-L,
解得:R=2L ,故A错误.
,故A错误.
B、电子在磁场中运动时间t=$\frac{T}{6}$,
周期:T=$\frac{2πR}{{v}_{0}}$,解得:t=$\frac{2πL}{3{v}_{0}}$.故B正确.
C、根据R=$\frac{m{v}_{0}}{qB}$=2L得,磁感应强度B=$\frac{m{v}_{0}}{2eL}$,故C正确.
D、电子在磁场中做匀速圆周运动,速度大小不变,方向在改变,故D错误.
故选:BC.
点评 本题考查了带电粒子在磁场中的运动,关键作出粒子的运动轨迹,确定圆心、半径、圆心角,结合半径公式和周期公式进行求解,难度中等.

练习册系列答案
相关题目
6.一质量为2kg的弹性小球,在光滑的水平面上以6m/s的速度垂直撞到墙上,碰撞后小球沿相反方向运动,反弹后的速度大小与碰撞前速度的大小相同,则碰撞前后小球速度变化量的大小△v和碰撞过程中墙对小球做功的大小W为( )
| A. | △v=0 | B. | △v=12m/s | C. | W=0 | D. | W=72J |
10.地球的质量为M、半径为R,地球表面的重力加速度为g,万有引力恒量为G,则第一宇宙速度为( )
| A. | $\sqrt{gR}$ | B. | $\sqrt{\frac{GMm}{{R}^{2}}}$ | C. | $\sqrt{\frac{GM}{R}}$ | D. | 2$\sqrt{gR}$ |
7.线圈在匀强磁场中匀速转动,产生交变电流的图象如图所示,由图中可知( )


| A. | 在A和C时刻线圈处于中性面位置 | |
| B. | 在B和D时刻穿过线圈的磁通量为零 | |
| C. | 在A~D时刻线圈转过的角度为2π | |
| D. | 若从O~D时刻经过0.02s,则在1s内交变电流的方向改变100次 |
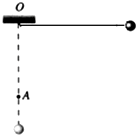 如图,长为l细绳的一端固定于O点,另一端系一个质量为m小球,使细绳偏离竖直方向90°(细绳处于伸直状态),由静止释放小球.已知小球经过最低点时对细绳的拉力为3mg.现在O点的正下方钉一个钉子A,小球仍从原来位置静止释放,当细绳与钉子相碰时,小球对细绳的拉力为6mg,求钉子与O点的距离(不计一切摩擦和空气阻力).
如图,长为l细绳的一端固定于O点,另一端系一个质量为m小球,使细绳偏离竖直方向90°(细绳处于伸直状态),由静止释放小球.已知小球经过最低点时对细绳的拉力为3mg.现在O点的正下方钉一个钉子A,小球仍从原来位置静止释放,当细绳与钉子相碰时,小球对细绳的拉力为6mg,求钉子与O点的距离(不计一切摩擦和空气阻力). 在“验证机械能守恒定律”的一次实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻记数点时间间隔为0.02s),那么:
在“验证机械能守恒定律”的一次实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻记数点时间间隔为0.02s),那么:
 如图所示,一个圆盘在水平面内匀速转动,角速度是4rad/s,盘面上距盘中心0.10m的位置有一个质量为10g的小物体与圆盘保持静止,跟着圆盘一起做匀速圆周运动.
如图所示,一个圆盘在水平面内匀速转动,角速度是4rad/s,盘面上距盘中心0.10m的位置有一个质量为10g的小物体与圆盘保持静止,跟着圆盘一起做匀速圆周运动.