Question

【题目】一个装盛某种液体的圆柱形铁桶，其中央纵截面是边长为a的正方形，如图16所示．当桶内没有液体时，从某点A恰能看到桶底边缘的某点B．当桶内液体的深度为桶高的 时，仍沿AB方向看去，恰好看到桶底上的C点，C、B两点相距 a，求该液体的折射率（最后结果可用根式表示）．

Answer 1

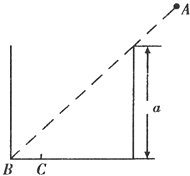
【答案】解：当液体的深度为桶高的 时，光路如图所示：

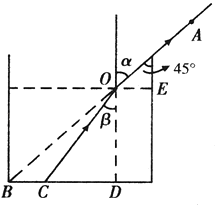
由几何关系，知：|OE|= a，|BC|= a，|CD|= a

所以：

|OC|= = a

则得sinα=sin45°= ，sinβ= =

根据折射定律表达式．该液体的析射率n为：

n= = =

答：该液体的折射率为 ．

【解析】首先画出光路图，再根据几何关系求出入射角和折射角正弦值，就可结合折射定律求出液体的折射率．
【考点精析】根据题目的已知条件，利用光的折射的相关知识可以得到问题的答案，需要掌握光由一种介质射入另一种介质时，在两种介质的界面上将发生光的传播方向改变的现象叫光的折射．