题目内容
设地球的半径为R ,质量为m的卫星在距地面3R高处绕地球做匀速圆周运动,已知地面处的重力加速度为g,则
A. 卫星的线速度为
B. 卫星的角速度为 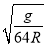
C. 卫星的加速度为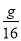
D. 卫星的周期为2π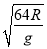
练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
题目内容
设地球的半径为R ,质量为m的卫星在距地面3R高处绕地球做匀速圆周运动,已知地面处的重力加速度为g,则
A. 卫星的线速度为
B. 卫星的角速度为 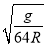
C. 卫星的加速度为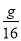
D. 卫星的周期为2π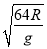
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案