题目内容
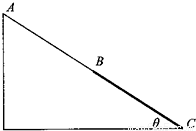
如图所示是游乐场中供小孩玩耍的滑梯简化图，斜面AC长10米，与水平面之间的夹角θ=30°，斜面上AB、BC两部分等长，BC部分表面改用塑胶垫．一小孩从斜面顶端A无初速下滑，设他与斜面AB之间的动摩擦因数u1=
，与BC之间的动摩擦因数u2=
，（取g=10m/s2）问：
（1）小孩从A点开始下滑到B点需要的时间以及通过B点时的速度大小；
（2）诵讨计算说明小孩能否滑到斜面的底端C处．
解：（1）小孩在AB段做匀加速直线运动，设加速度为a1，则
mgsinθ-μ1mgcosθ=ma1
解得：a1=2.5m/s2
又因为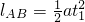
解得：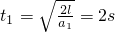
故vB=a1t1=5m/s
（2）小孩在BC段运动的加速度为a2，则
mgsinθ-μ2mgcosθ=ma2
解得：
即小孩做匀减速运动，设最终停在斜面上，其减速运动的位移为x，
0-
解得：x=5m
所以小孩的最大位移为l总=l+x=10m，恰好到达斜面底端．
答：（1）小孩从A点开始下滑到B点需要的时间以及通过B点时的速度大小为5m/s；
（2）小孩恰好滑到斜面的底端C处．
分析：（1）小孩在AB段做匀加速直线运动，根据牛第二定律求出加速度，根据位移时间公式求出时间，再根据速度时间公式即可求得速度；
（2）根据牛第二定律求出小孩在BC段的加速度，设最终停在斜面上，求出运动的位移，再跟BC段长度比较即可求解．
点评：本题主要考查了匀变速直线运动基本公式的直接应用，本题解答时也可以根据动能定理求解，难度适中．
mgsinθ-μ1mgcosθ=ma1
解得：a1=2.5m/s2
又因为
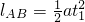
解得：
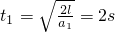
故vB=a1t1=5m/s
（2）小孩在BC段运动的加速度为a2，则
mgsinθ-μ2mgcosθ=ma2
解得：
即小孩做匀减速运动，设最终停在斜面上，其减速运动的位移为x，
0-
解得：x=5m
所以小孩的最大位移为l总=l+x=10m，恰好到达斜面底端．
答：（1）小孩从A点开始下滑到B点需要的时间以及通过B点时的速度大小为5m/s；
（2）小孩恰好滑到斜面的底端C处．
分析：（1）小孩在AB段做匀加速直线运动，根据牛第二定律求出加速度，根据位移时间公式求出时间，再根据速度时间公式即可求得速度；
（2）根据牛第二定律求出小孩在BC段的加速度，设最终停在斜面上，求出运动的位移，再跟BC段长度比较即可求解．
点评：本题主要考查了匀变速直线运动基本公式的直接应用，本题解答时也可以根据动能定理求解，难度适中．
练习册系列答案
相关题目
如图所示是游乐场中供小孩玩耍的滑梯简化图，斜面AC长10米，与水平面之间的夹角θ=30°，斜面上AB、BC两部分等长，BC部分表面改用塑胶垫．一小孩从斜面顶端A无初速下滑，设他与斜面AB之间的动摩擦因数u1=
＝30°，斜面上AB、BC两部分等长，BC部分表面改用塑胶垫．一小孩从斜面顶端A无初速下滑，设他与斜面AB之间的动摩擦因数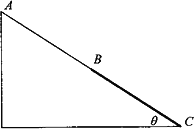
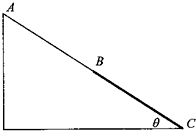
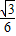，与BC之间的动摩擦因数
，(取g＝10 m/s2)问：
，与BC之间的动摩擦因数u2=
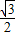，（取g=10m/s2）问：