题目内容
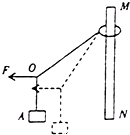
【题目】如图所示,一辆卡车后面用轻绳拖着质量为m的物体A,A与地面的摩擦不计.求: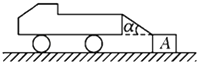
(1)当卡车以a1= ![]() g的加速度运动时,绳的拉力为
g的加速度运动时,绳的拉力为 ![]() mg,则A对地面的压力?
mg,则A对地面的压力?
(2)当卡车的加速度a2=g时,绳的拉力?
【答案】
(1)解:卡车和A的加速度一致,由图知绳的拉力的分力使A产生了加速度,故有: ![]() mgcosα=
mgcosα= ![]() mg
mg
解得:cosα= ![]() ,sinα=
,sinα= ![]() 设地面对A的支持力为FN,则有:
设地面对A的支持力为FN,则有:
FN=mg﹣ ![]() mgsinα=
mgsinα= ![]() mg
mg
由牛顿第三定律得:A对地面的压力为 FN′=FN= ![]() mg.
mg.
答: A对地面的压力为 ![]() mg
mg
(2)解:设地面对A弹力为零时,物体的临界加速度为a0,则a0=gcotα= ![]() g
g
故当a2=g>a0时,物体已飘起,此时物体所受合力为mg,则由三角形知识可知,拉力F2= ![]() =
= ![]() mg
mg
答:绳的拉力为 ![]() mg
mg
【解析】(1)卡车和A的加速度一致,由图知绳的拉力的分力使A产生了加速度,根据牛顿第二定律求出夹角的正弦和余弦值,设地面对A的支持力为FN,根据竖直方向受力平衡即可求解;(2)先求出地面对A弹力为零时物体的加速度,再跟g进行比较,确定物体的状态,再由三角形知识即可求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目