题目内容
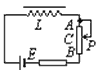
【题目】如图所示，地面上方有一水平光滑的平行导轨，导轨左侧有一固定挡板，质量M=2Kg的小车紧靠挡板右侧。长L=0.45m的轻质刚性绳一端固定在小车底部的O点，另一端栓接质量m=1Kg的小球。将小球拉至于O点等高的A点，使绳伸直后由静止释放，取重力加速度g=10m/s2.
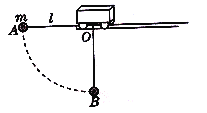
（1）求小球经过O点正下方的B点时，绳的拉力大小；
（2）若在小车速度最大时剪断细绳，小球落地，落地位置与小球剪断细绳时的位置间的水平距离s=1m，求滑轨距地面的高度。
【答案】（1）
(2)
【解析】（1）从A到B的过程应用动能定理得：
在B点，由牛顿第二定律得：
代入数据的F=30N
（2）由相互作用可知，小车速度最大时，小球一定在O点正下方。绳断后，小球做平抛运动，设此时小车速度为
，小球速度为
。水平方向上，以小车和小球组成的系统为研究对象，由水平方向上动量守恒定律得：
对小车与小球，由机械能守恒定律得：
由平抛运动规律得：
， 
则滑轨高度
代入数据得：H=5.45m
练习册系列答案
相关题目
