题目内容
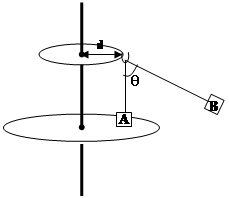
如图, 上下两个转盘可绕穿过它们中心的竖直轴水平转动，且两盘角速度相同, 其中上盘的半径为d。一根不计重力的轻绳两端分别系有A、B两物体，质量分别为2m和m。将轻绳跨过固定在上转盘边缘的光滑挂钩，挂钩与B物体间的一段绳子长为L。当两个转盘以角速度ω匀速转动时,两段轻绳与转轴在同一竖直平面内,一段轻绳与竖直方向的夹角为θ，另一段轻绳始终沿竖直方向。（g=10m/s²，sin53°=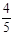
,cos53°=
）
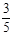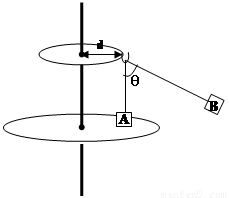
（1）求转盘转动的角速度ω与夹角θ的关系？
（2）当转盘的角速度缓慢增加的过程中，夹角θ如何变化？A物体受到的摩擦力如何变化？试分析。
（3）已知B物体端的绳长L=4.5m,上盘半径d=0.4m。当角速度增加到某一数值时，B物体端的轻绳与竖直方向的夹角为53°，此时A物体恰好开始滑动，求A物体与下盘之间的动摩擦因数µ ？（最大静摩擦力等于滑动摩擦力）
【答案】
略
【解析】略
练习册系列答案
同步练习强化拓展系列答案
相关题目
