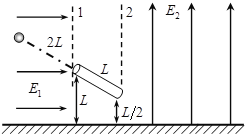Question

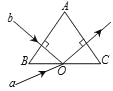
【题目】如图所示，一倾角θ＝30的光滑斜面上水平固定一玻璃挡板（玻璃挡板与地面平行）和垂直斜面的光滑小圆柱A和B， A、B连线水平．质量分别为2m和6m的p、q两小球用柔软细绳连接，小球q置于玻璃挡板处，细绳跨过圆柱A、B并拉直．将小球p从图示位置由静止释放，当玻璃挡板恰好不受压力时，p球摆过的角度为α．则

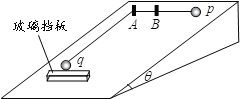
A.α＝30

B.α＝90

C.此过程中p球重力的功率先增大后减小

D.此过程中p球重力的功率一直增大

Answer 1

【答案】BC

【解析】

根据玻璃挡板恰好不受压力时，可分析出q球的受力，即可得到绳子的拉力，在对p球进行受力分析，列出向心力的表达式，结合动能定理即可解决相关问题。

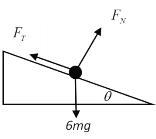
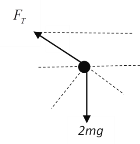
AB．当玻璃挡板恰好不受压力时，对小球q受力分析如下图，可得：

对小球p分析，p球摆过的角度为α时速度为v，沿斜面方向看，可得：

由动能定理得：

，

联立上式解得：

，则

CD． p小球从静止释放，p球开始重力的功率，当摆过时，重力方向和速度方向垂直，根据，由此重力的功率先增大后减小，C正确，D错误；

故选BC。