题目内容
9. 在如图所示的圆锥摆中,圆锥小球的质量为m,细绳长度为l,小球运动过程中学生与竖直方向的夹角为θ.则小球做圆周运动的周期T=$2π\sqrt{\frac{lcosθ}{g}}$;细绳的拉力大小F=$\frac{mg}{cosθ}$.
在如图所示的圆锥摆中,圆锥小球的质量为m,细绳长度为l,小球运动过程中学生与竖直方向的夹角为θ.则小球做圆周运动的周期T=$2π\sqrt{\frac{lcosθ}{g}}$;细绳的拉力大小F=$\frac{mg}{cosθ}$.
分析 小球在重力和拉力合力作用下做圆周运动,靠两个力的合力提供向心力,根据牛顿第二定律求出周期的大小.
解答 解:小球受重力和拉力作用,两个力的合力提供向心力,根据合成法得:Fcosθ=mg
所以:F=$\frac{mg}{cosθ}$
根据牛顿第二定律得:mgtanθ=mr$(\frac{2π}{T})^{2}$
又 r=lsinθ
整理得:T=$2π\sqrt{\frac{lcosθ}{g}}$
故答案为:$2π\sqrt{\frac{lcosθ}{g}}$,$\frac{mg}{cosθ}$
点评 解决本题的关键搞清小球做圆周运动向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
19.某同学得到一个未知元件,想要描绘它的伏安特性曲线.
(1)图1是实验器材,请画线将其连成实验电路.要求:实验过程中,滑动变阻器的滑片从a端滑到b端,电压表的示数逐渐变大;测量电路采用电流表外接法.
(2)实验测得该元件两端的电压U和通过它的电流I的数据如下表所示.
根据表中数据,在图2坐标纸上选择恰当标度,画出该元件的I-U图线.
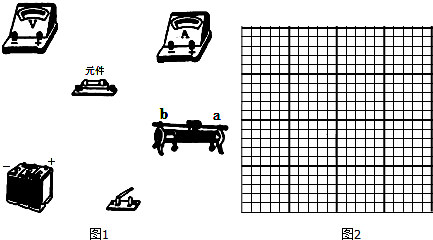
(3)根据该元件的I-U图线,请描述该元件的电阻随加在该元件两端电压的变化规律:该元件的电阻随元件两端电压的增大而减小.
(1)图1是实验器材,请画线将其连成实验电路.要求:实验过程中,滑动变阻器的滑片从a端滑到b端,电压表的示数逐渐变大;测量电路采用电流表外接法.
(2)实验测得该元件两端的电压U和通过它的电流I的数据如下表所示.
| U/V | 0 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 |
| I/mA | 0 | 0.9 | 2.3 | 4.3 | 6.8 | 12.0 | 19.0 | 30.0 |

(3)根据该元件的I-U图线,请描述该元件的电阻随加在该元件两端电压的变化规律:该元件的电阻随元件两端电压的增大而减小.
20. 如图所示,两物体的质量m1>m2,不计一切摩擦及滑轮的质量,由静止放手后让m1、m2运动时,细绳上拉力F的大小( )
如图所示,两物体的质量m1>m2,不计一切摩擦及滑轮的质量,由静止放手后让m1、m2运动时,细绳上拉力F的大小( )
 如图所示,两物体的质量m1>m2,不计一切摩擦及滑轮的质量,由静止放手后让m1、m2运动时,细绳上拉力F的大小( )
如图所示,两物体的质量m1>m2,不计一切摩擦及滑轮的质量,由静止放手后让m1、m2运动时,细绳上拉力F的大小( )| A. | 小于mlg | B. | 等于mlg | C. | 等于$\frac{{{m_1}g+{m_2}g}}{2}$ | D. | 大于m1g |
17. 如图,一质量为m、半径为r的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上的小环(质量也为m,可视为质点),从大环的最高处由静止滑下.重力加速度大小为g,当小环滑到大环的最低点时,大环对轻杆拉力的大小为6mg,则此时小环的速度大小为( )
如图,一质量为m、半径为r的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上的小环(质量也为m,可视为质点),从大环的最高处由静止滑下.重力加速度大小为g,当小环滑到大环的最低点时,大环对轻杆拉力的大小为6mg,则此时小环的速度大小为( )
 如图,一质量为m、半径为r的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上的小环(质量也为m,可视为质点),从大环的最高处由静止滑下.重力加速度大小为g,当小环滑到大环的最低点时,大环对轻杆拉力的大小为6mg,则此时小环的速度大小为( )
如图,一质量为m、半径为r的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上的小环(质量也为m,可视为质点),从大环的最高处由静止滑下.重力加速度大小为g,当小环滑到大环的最低点时,大环对轻杆拉力的大小为6mg,则此时小环的速度大小为( )| A. | $\sqrt{gr}$ | B. | 2$\sqrt{gr}$ | C. | $\sqrt{6gr}$ | D. | $\sqrt{5gr}$ |
4.如图所示,宇航员在围绕地球做匀速圆周运动的空间站中会完全失重,下列说法中正确的是( )

| A. | 宇航员受力平衡 | |
| B. | 宇航员不受任何作用力 | |
| C. | 宇航员仍受万有引力的作用 | |
| D. | 宇航员受的万有引力正好提供向心力 |
14.如图是发电机的原理示意图,线圈abcd在匀速转动的过程中,下列判断正确的是( )


| A. | 通过R的电流是直流电 | |
| B. | 线圈经过中性面时,产生的感应电动势最大 | |
| C. | 线圈经过中性面时,穿过线圈的磁通量为0 | |
| D. | 线圈经过中性面时,通过R的电流方向将改变 |
7.下列说法正确的是( )
| A. | 光电效应实验揭示了光的粒子性 | |
| B. | 按照波尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,但原子的能量增大 | |
| C. | 一束光照射到某种金属上不能发生光电效应,可能是因为这束光的波长太短 | |
| D. | 原子核发生一次β衰变,就会增加一个质子 | |
| E. | 氢原子从低能级跃迁到高能级要放出能量 |
 如图所示,在点电荷+Q电场中的一条电场线上取a、b两点,Oa=$\frac{1}{4}$Ob,当在a处放一电荷量q=1.5×10-8 C带正电的试探电荷时,受到的静电力为F=3×10-6 N.
如图所示,在点电荷+Q电场中的一条电场线上取a、b两点,Oa=$\frac{1}{4}$Ob,当在a处放一电荷量q=1.5×10-8 C带正电的试探电荷时,受到的静电力为F=3×10-6 N.