题目内容
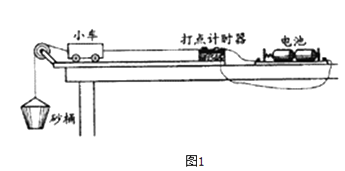
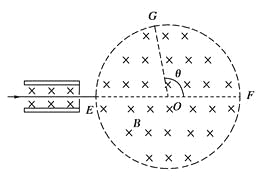
【题目】某实验小组欲以图甲所示实验装置“探究加速度与物体受力和质量的关系”.图中A为小车，B为装有砝码的小盘，C为一端带有定滑轮的长木板，小车通过纸带与打点计时器相连，小车的质量为
，小盘(及砝码)的质量为
.
（1）下列说法正确的是（______）
A．实验时先放开小车，再接通打点计时器的电源
B．每次改变小车质量时，应重新平衡摩擦力
C．本实验中应满足
远小于
的条件
D．在用图象探究小车加速度与质量的关系时，应作
图象
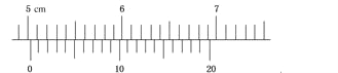
（2）实验中，得到一条打点的纸带，如图乙所示，已知相邻计数点间的时间间隔为T，且间距
、
、
、
、
、
已量出，则小车加速度的计算式a=________________________.
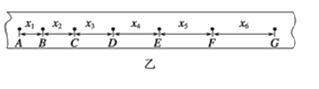
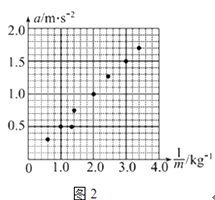
（3）某同学平衡好摩擦阻力后，在保持小车质量不变的情况下，通过多次改变砝码重力，作出小车加速度a与砝码重力F的图象如图丙所示.若牛顿第二定律成立，重力加速度
，则小车的质量为__________ 
，小盘的质量为__________ 
.(保留2位有效数字)
（4）实际上，在砝码的重力越来越大时，小车的加速度不能无限制地增大，将趋近于某一极限值，此极限值为___________
. (
)
【答案】 C 
2.0 0.060 10
【解析】解: (1)A．实验时先接通打点计时器的电源，再放开小车,A错误
B．每次改变小车质量时，不需要重新平衡摩擦力 B错误
C．只有满足m2应远小于m1的条件,才能认为托盘和砝码的重力等于小车的拉力,故C正确。
D、“探究加速度与质量的关系”时拉力不变,即m1不变,应作
图象,故D错误
(2)根据匀变速直线运动的推论公式
,六组数据应该用逐差法求平均加速度,因此在本题中有: 
(3)对
图象来说,图象的斜率表示小车质量的倒数,图象的斜率为: 
,故小车质量为: 
,F=0时,产生的加速度是由于托盘作用产生的,故有: 
,解得: 
(对图中的数据读取不一样,可有一定范围).
(4)当钩码的质量远小于小车的总质量时,钩码所受的重力才能作为小车所受外力,如果增大钩码的质量,则外力增大,曲线不断延伸,那么加速度趋向为g=10m/s2。
新非凡教辅冲刺100分系列答案【题目】某物理兴趣小组利用传感器进行探究实验，其实验装置及原理图分别如甲、乙所示．
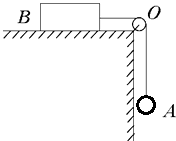
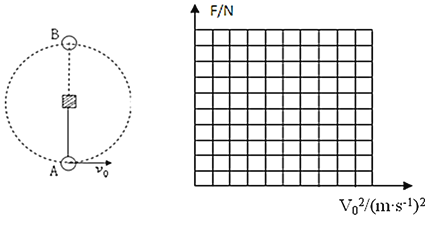
该装置中，A、B为力传感器，研究对象是质量m=310g的金属圆柱体G，将G放在A、B的两探头之间，两探头受到压力的数据，通过传感器、数据采集器传输给计算机，数据如表1所示．
表1 圆柱体的质量：310g
θ/° | 0 | 30 | 45 | 60 | 90 |
FA/N | 0.00 | 1.49 | 2.12 | 2.59 | 3.02 |
FB/N | 3.01 | 2.61 | 2.13 | 1.50 | 0.00 |
（1）观察、分析数据表1，可得出：金属圆柱体重力沿斜面向下的分力FA随斜面倾角θ的增大而 ， 垂直斜面向下的分力FB随斜面倾角θ的增大而 ．
（2）某同学发现两传感器的读数并不是与角度的变化成正比，他猜想圆柱体所受重力及其分力间满足某个函数关系，并根据该函数关系计算两探头受到压力的理论值如表2所示（g取9.8m/s2）
表2 圆柱体的质量：310g
θ/° | 0 | 30 | 45 | 60 | 90 |
FA/N | 0.00 | 1.52 | 2.15 | 2.63 | 3.04 |
FB/N | 3.04 | 2.63 | 2.15 | 1.52 | 0.00 |
该同学猜测的函数关系式应当分别为：FA= ， FB=（用金属圆柱体质量m、重力加速度g、斜面倾角θ表示）
（3）在实验中无论是分析“表1”还是“表2”的数据时，都认为传感器的读数都等于相应的圆柱体重力的分力，其物理学依据是（乙沿斜面方向为例）；因为A传感器的读数等于A传感器所受的压力，根据此压力大小等于圆柱体沿斜面方向所受的支持力，而根据此支持力大小等于圆柱体重力沿斜面方向的分力
（4）为了减少实验误差，可采取的办法是（写出一个即可）
