题目内容
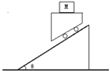
 如图所示:小车沿倾角为θ的光滑斜面滑下,在小车的水平台面上有一质量为M的木块和小车保持相对静止,则( )
如图所示:小车沿倾角为θ的光滑斜面滑下,在小车的水平台面上有一质量为M的木块和小车保持相对静止,则( )分析:对整体分析可知整体运动的加速度,再M受力分析可知M受力情况; 再根据功的定义可得出支持力做的功.
解答:解:A、对整体受力分析可知,整体受重力、支持力其合力沿斜面向下,加速度a=gsinθ; 再对M分析,可知,M的合力为F=mgsinθ,沿斜面向下,而重力和支持力的合力只能沿竖直方向,水平方向只能为小车对M的摩擦力,故摩擦力等于重力水平方向的分力f=mgsinθcosθ,故A正确;
B、小车合力在竖直方向的分力不为零,故重力与支持力的合力不为零,故重力不等于支持力,故B错误;
C、小车受重力、支持力、压力、M对小车的摩擦力,故小车受四个力,故C正确;
D、支持力竖直向上,与物体的位移的方向成钝角,故支持力对M做负功,故D错误;
故选AC.
B、小车合力在竖直方向的分力不为零,故重力与支持力的合力不为零,故重力不等于支持力,故B错误;
C、小车受重力、支持力、压力、M对小车的摩擦力,故小车受四个力,故C正确;
D、支持力竖直向上,与物体的位移的方向成钝角,故支持力对M做负功,故D错误;
故选AC.
点评:本题考查功及牛顿第二定律的综合,注意在分解合力时,可以将力或加速度分解,从而求出可能的分力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,小车沿倾角为θ的斜面做匀加速直线运动,小车支架上有一单摆,在运动过程中,摆线为水平状态,则小车运动的加速度大小为( )
如图所示,小车沿倾角为θ的斜面做匀加速直线运动,小车支架上有一单摆,在运动过程中,摆线为水平状态,则小车运动的加速度大小为( )