题目内容
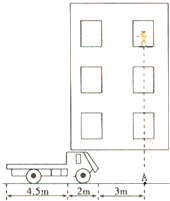 如图所示,一只猫在离地面高h1=6m的楼房窗口处从静止开始自由下落,其正下方地面为A点.若有一辆平板汽车正以V0=6m/s的速度向A点匀速前进.已知猫刚下落时,平板汽车恰好运动到车前端距A点3m处,该汽车车头长2m,汽车平板长4.5m,平板车板面离地面高h2=1m,猫可看作质点,取g=10m/s2,猫下落过程中未与汽车车头接触,猫与平板车板面间的动摩擦因数为μ=0.2,求:
如图所示,一只猫在离地面高h1=6m的楼房窗口处从静止开始自由下落,其正下方地面为A点.若有一辆平板汽车正以V0=6m/s的速度向A点匀速前进.已知猫刚下落时,平板汽车恰好运动到车前端距A点3m处,该汽车车头长2m,汽车平板长4.5m,平板车板面离地面高h2=1m,猫可看作质点,取g=10m/s2,猫下落过程中未与汽车车头接触,猫与平板车板面间的动摩擦因数为μ=0.2,求:(1)猫将落在平板车上距车尾端多远处?
(2)假定猫落到车平板上后立即俯卧在车上不弹起,司机同时使车开始以大小为a1=4m/s2的加速度做匀减速直线运动,直到停止,则猫是否会从平板车上滑下?若会滑下,请计算说明原因;若不会滑下,则猫最终停在距车尾端多远处?
分析:(1)猫跳下后做自由落体运动,根据运动学基本公式求出下落过程中时间和平板汽车运动的位移,进而求出猫在车上的落点距车尾端距离;
(2)根据牛顿第二定律求出猫在车平板上的加速度,设猫未滑下,且经时间t′猫与车达到相等的速度v,根据运动学基本公式即可判断.
(2)根据牛顿第二定律求出猫在车平板上的加速度,设猫未滑下,且经时间t′猫与车达到相等的速度v,根据运动学基本公式即可判断.
解答:解:(1)设猫下落时间为t,则h1-h2=
gt2
车在时间t内运动的位移x=v0t
代入数据解得x=6m
猫在车上的落点距车尾端距离d=(3+2+4.5)m-6 m=3.5 m
(2)猫落在平板车上后,水平方向做匀加速直线运动,车做匀减速直线运动,设经时间t′猫与车达到相等的速度;
猫的加速度为a2=μg=2m/s2 则:v0+a1t′=a2t
解得:t′=
=
=1s;
此时的速度均为:v=a2t′=2×1=2m/s
猫和车的相对位移为:△S=S车-S猫=v0t′+
a1t′2-
a2t′2=6×1+
×(-4)×1-
×2×1=3m<3.5m
故不会滑下,即速度相等时,猫在距车尾端3.5-3=0.5m远处
猫与车达到相等的速度后,车向前减速直至停止的位移S′车=
=
=0.5m
猫向前减速直至停止的位移S′猫=
=
=1m
猫相对车再次向前滑动:△S′=S车′-S猫′=1-0.5=0.5m
故猫与车速度相等后,会再次相对车向前运动0.5m,最终停在距车尾1.0m远处
答:(1)猫将落在平板车上距车尾端3.5m处;
(2)猫不会从平板车上滑下,猫最终停在距车尾端1m远处.
| 1 |
| 2 |
车在时间t内运动的位移x=v0t
代入数据解得x=6m
猫在车上的落点距车尾端距离d=(3+2+4.5)m-6 m=3.5 m
(2)猫落在平板车上后,水平方向做匀加速直线运动,车做匀减速直线运动,设经时间t′猫与车达到相等的速度;
猫的加速度为a2=μg=2m/s2 则:v0+a1t′=a2t
解得:t′=
| v0 |
| a2-a1 |
| 6 |
| 2+4 |
此时的速度均为:v=a2t′=2×1=2m/s
猫和车的相对位移为:△S=S车-S猫=v0t′+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故不会滑下,即速度相等时,猫在距车尾端3.5-3=0.5m远处
猫与车达到相等的速度后,车向前减速直至停止的位移S′车=
| v2 |
| 2a1 |
| 22 |
| 2×4 |
猫向前减速直至停止的位移S′猫=
| v2 |
| 2a2 |
| 22 |
| 2×2 |
猫相对车再次向前滑动:△S′=S车′-S猫′=1-0.5=0.5m
故猫与车速度相等后,会再次相对车向前运动0.5m,最终停在距车尾1.0m远处
答:(1)猫将落在平板车上距车尾端3.5m处;
(2)猫不会从平板车上滑下,猫最终停在距车尾端1m远处.
点评:本题主要考查了自由落体运动、匀变速直线运动的基本公式的直接应用,要求同学们能正确分析车和猫的运动情况,较难.

练习册系列答案
相关题目


 C.
C. D.
D.

 A.g B.
A.g B.
 D.
D.
 如图所示,一只猫在离地面高h1=6m的楼房窗口处从静止开始自由下落,其正下方地面为A点.若有一辆平板汽车正以V0=6m/s的速度向A点匀速前进.已知猫刚下落时,平板汽车恰好运动到车前端距A点3m处,该汽车车头长2m,汽车平板长4.5m,平板车板面离地面高h2=1m,猫可看作质点,取g=10m/s2,猫下落过程中未与汽车车头接触,猫与平板车板面间的动摩擦因数为μ=0.2,求:
如图所示,一只猫在离地面高h1=6m的楼房窗口处从静止开始自由下落,其正下方地面为A点.若有一辆平板汽车正以V0=6m/s的速度向A点匀速前进.已知猫刚下落时,平板汽车恰好运动到车前端距A点3m处,该汽车车头长2m,汽车平板长4.5m,平板车板面离地面高h2=1m,猫可看作质点,取g=10m/s2,猫下落过程中未与汽车车头接触,猫与平板车板面间的动摩擦因数为μ=0.2,求: