题目内容
18．
光滑水平面上放着物块A与质量为m的物块B，A与B均可视为质点，A靠在竖直墙壁上，A、B间夹一个被压缩的轻弹簧（弹簧与A、B均不拴接），用手挡住B不动，此时弹簧压缩了一定长度，如下图所示，放手后弹簧将物块B迅速弹出，B向右运动，之后B冲上与水平面相切的竖直半圆光滑轨道，其半径R=0.5m，B恰能到达最高点C．取g=10m/s2，求物块B的落点距离C的水平距离．
分析 B球恰好能到达最高点，结合牛顿第二定律求出最高点的速度，根据高度求出平抛运动的时间，结合初速度和时间求出落点与C的水平距离．
解答 解：B球恰好能够到达最高点C，根据牛顿第二定律得，$mg=m\frac{{{v}_{C}}^{2}}{R}$，
解得${v}_{C}=\sqrt{gR}$=$\sqrt{10×0.5}m/s=\sqrt{5}m/s$，
根据2R=$\frac{1}{2}g{t}^{2}$得，t=$\sqrt{\frac{4R}{g}}=\sqrt{\frac{4×0.5}{10}}=\frac{\sqrt{5}}{5}s$，
则水平距离x=${v}_{C}t=\sqrt{5}×\frac{\sqrt{5}}{5}m=1m$．
答：物块B的落地点距离C的水平距离为1m．
点评 本题考查了圆周运动和平抛运动的基本运用，知道圆周运动向心力的来源和平抛运动在水平方向和竖直方向上的运动规律是解决本题的关键．
练习册系列答案
相关题目
如图所示，质量为m=0.2kg的小球固定在长为L=0.9m的轻杆的一端，杆可绕O点的水平转轴在竖直平面内转动．g=10m/s2，求：
如图所示，在长约100cm一端封闭的玻璃管中注满清水，水中放一个用红蜡做成的小圆柱体（小圆柱体恰能在管中匀速上浮），将玻璃管的开口端用胶塞塞紧．然后将玻璃管竖直倒置，在红蜡块匀速上浮的同时使玻璃管紧贴黑板面水平向右匀加速移动，你正对黑板面将看到红蜡块相对于黑板面的移动轨迹可能是下面的（ ）
3．关于多普勒效应，下列说法中正确的是（ ）
| A． | 只要波源在运动，就一定能观察到多普勒效应 | |
| B． | 只要观察者在运动，就一定能观察到多普勒效应 | |
| C． | 只要波源与观察者之间有相对运动，就能观察到多普勒效应 | |
| D． | 当发生多普勒效应时，观察者感到的频率可能增大也可能减小 |
10．
在平直公路上，汽车由静止开始做匀加速运动，当速度达到vm后立即关闭发动机直到停止，v-t图象如图所示．设汽车的牵引力为F，摩擦力为Ff，全过程中牵引力做功W1，克服摩擦力做功W2，则（ ）
在平直公路上，汽车由静止开始做匀加速运动，当速度达到vm后立即关闭发动机直到停止，v-t图象如图所示．设汽车的牵引力为F，摩擦力为Ff，全过程中牵引力做功W1，克服摩擦力做功W2，则（ ）| A． | F：Ff=1：3 | B． | F：Ff=4：3 | C． | W1：W2=1：1 | D． | W1：W2=1：3 |
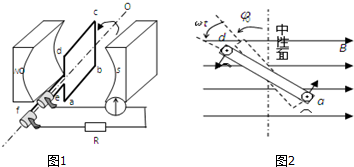
如图所示，水平导轨间距为L=0.5m，导轨电阻忽略不计；导体棒ab的质量m=l kg，电阻R0=0.9Ω，与导轨接触良好；电源电动势E=10V，内阻r=0.1Ω，电阻R=4Ω；外加匀强磁场的磁感应强度B=5T，方向垂直于ab，与导轨平面成α=53°角；ab与导轨间动摩擦因数为μ=0.5（设最大静摩擦力等于滑动摩擦力），定滑轮摩擦不计，线对ab的拉力为水平方向，重力加速度g=10m/s2，ab处于静止状态．已知sin53°=0.8，cos53°=0.6．求：