题目内容
如图所示，质量为m=0.1kg的小球和A、B两根细绳相连，两绳固定在细杆的A、B两点，其中A绳长LA=2m，当两绳都拉直时，A、B两绳和细杆的夹角θ1=30°，θ2=45°，g=10m/s2．求：
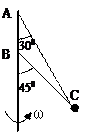
（1）当细杆转动的角速度ω在什么范围内，A、B两绳始终张紧？
（2）当ω=3rad/s时，A、B两绳的拉力分别为多大？
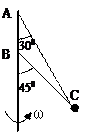
（1）当细杆转动的角速度ω在什么范围内，A、B两绳始终张紧？
（2）当ω=3rad/s时，A、B两绳的拉力分别为多大？
（1）ω2=3.15（rad/s）
要使两绳都拉紧2.4 rad/s≤ω≤3.15 rad/s
（2）TA=0.27N， TB=1.09N
要使两绳都拉紧2.4 rad/s≤ω≤3.15 rad/s
（2）TA=0.27N， TB=1.09N
（1）当B绳恰好拉直，但TB=0时，细杆的转动角速度为ω1，
有： TAcos30°=mg
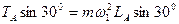
解得：ω1=2．4rad/s
当A绳恰好拉直，但TA=0时，细杆的转动角速度为ω2，
有：
解得：ω2=3.15（rad/s）
要使两绳都拉紧2.4 rad/s≤ω≤3.15 rad/s
（2）当ω="3" rad/s时，两绳都紧．
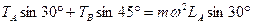
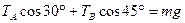
TA=0.27N， TB=1.09N
[点评]分析两个极限（临界）状态来确定变化范围，是求解“范围”题目的基本思路和方法．
有： TAcos30°=mg
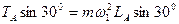
解得：ω1=2．4rad/s
当A绳恰好拉直，但TA=0时，细杆的转动角速度为ω2，
有：
解得：ω2=3.15（rad/s）
要使两绳都拉紧2.4 rad/s≤ω≤3.15 rad/s
（2）当ω="3" rad/s时，两绳都紧．
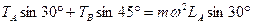
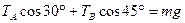
TA=0.27N， TB=1.09N
[点评]分析两个极限（临界）状态来确定变化范围，是求解“范围”题目的基本思路和方法．
练习册系列答案
相关题目
．
，
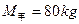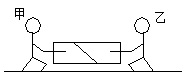
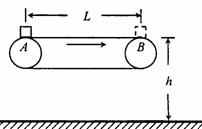
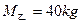，面对面拉着弹簧秤做匀速圆周运动的滑冰表演，如图所示，两人相距0.9m，弹簧秤的示数为9.2N，下列判断中正确的是
