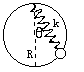题目内容
如图所示,一原长为L0的轻质弹簧下端固定在水平地面上,其上端与一质量为m的重物相连接,当重物静止时,弹簧保持竖直方向,长度为L1.现用力缓慢竖直向下将重物压至D点,此时弹簧长度为L2,外力大小为F.然后撤去外力,重物将从静止开始沿竖直方向在D、C之间做简谐振动,B是D、C的中点.已知重物运动到D点时弹簧的弹性势能为EP0,运动到B点时的物体的动能为EKB.则外力开始时将重物压至D点的过程中所做的功为( )
A.EKB B.EP
A
解析:当物体静止于弹簧上时,有kx=mg,x为弹簧的压缩量,当弹簧在外力撤除后做简谐振动时,其平衡位置扫处对应弹簧的压缩量也为x,由能量守恒可得:此时物体
在B处的动能即外力对物体做的功,W=EKB,A正确;因压缩弹簧过程中,外力F为变力作用,故不能利用C、D式进行求解.而弹簧在D点处的弹性势能是由外力的功及重力势能的降低两部分转化而来,B错.

练习册系列答案
相关题目
 如图所示,一长木板质量为M=4kg,木板与地面的动摩擦因数μ1=0.2,质量为m=2kg的小滑块放在木板的右端,小滑块与木板间的动摩擦因数μ2=0.4.开始时木板与滑块都处于静止状态,木板的右端与右侧竖直墙壁的距离L=2.7m.现给木板以水平向右的初速度v0=6m/s使木板向右运动,设木板与墙壁碰撞时间极短,且碰后以原速率弹回,取g=10m/s2,求:
如图所示,一长木板质量为M=4kg,木板与地面的动摩擦因数μ1=0.2,质量为m=2kg的小滑块放在木板的右端,小滑块与木板间的动摩擦因数μ2=0.4.开始时木板与滑块都处于静止状态,木板的右端与右侧竖直墙壁的距离L=2.7m.现给木板以水平向右的初速度v0=6m/s使木板向右运动,设木板与墙壁碰撞时间极短,且碰后以原速率弹回,取g=10m/s2,求: