题目内容
(1)紫外线照射一些物质时,会发生荧光效应,即物质发出可见光.这些物质中的原子先后发生两次跃迁,其能量变化分别为△E1和△E2.下列关于原子这两次跃迁的说法中正确的是______.A.两次均向高能级跃迁,且|△E1|>|△E2|
B.两次均向低能级跃迁,且|△E1|<|△E2|
C.先向高能级跃迁,再向低能级跃迁,且|△E1|<|△E2|
D.先向高能级跃迁,再向低能级跃迁,且|△E1|>|△E2|
(2)甲、乙两小孩各乘一辆小车在光滑水平面上匀速相向行驶,速度均为6m/s.甲车上有质量为m=1kg的小球若干个,甲和他的车及所带小球的总质量为M1=50kg,乙和他的车总质量为M2=30kg.现为避免相撞,甲不断地将小球以相对地面16.5m/s的水平速度抛向乙,且被乙接住.假设某一次甲将小球抛出且被乙接住后刚好可保证两车不致相撞,试求此时:
①两车的速度各为多少?
②甲总共抛出了多少个小球?
【答案】分析:(1)根据能级跃迁过程能量守恒和可见光和紫光的能量关系解决问题.
(2)甲、乙两小孩及两车组成的系统总动量守恒,当甲和小车与乙和小车具有共同速度时,可保证刚好不撞.
系统总动量守恒,但对于每一个小球被乙接收后,乙的动量发生改变,两者结合解决问题.
解答:解:(1):原子吸收紫外线,使原子由低能级向高能级跃迁,吸收△E1,再由高能级向低能级跃迁,放出可见光,由于紫外线光子能量大于可见光,故△E1>△E2,
故选D
(2)解:甲、乙两小孩依在抛球的时候是“一分为二”的过程,接球的过程是“合二为一”的过程.
(1)甲、乙两小孩及两车组成的系统总动量沿甲车的运动方向,甲不断抛球、乙接球后,当甲和小车与乙和小车具有共同速度时,可保证刚好不撞.设共同速度为V,则:
M1V1-M2V1=(M1+M2)V
v=1.5m/s
(2)这一过程中乙小孩接球的动量变化为:△P=30×6-30×(-1.5)=225(kg?m/s)
每一个小球被乙接收后,到最终的动量变化为△P1=16.5×1-1.5×1=15(kg?m/s)
故小球个数为 N=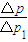 =15
=15
答:①两车的速度各为1.5m/s
②甲总共抛出了15个小球.
点评:(1)本题考查原子跃迁与能级能量变化及辐射或光子能量的关系.要明确色光间的波长及频率关系.
(2)解决问题首先要清楚研究对象的运动过程.利用动量守恒定律解题,一定注意状态的变化和状态的分析.
(2)甲、乙两小孩及两车组成的系统总动量守恒,当甲和小车与乙和小车具有共同速度时,可保证刚好不撞.
系统总动量守恒,但对于每一个小球被乙接收后,乙的动量发生改变,两者结合解决问题.
解答:解:(1):原子吸收紫外线,使原子由低能级向高能级跃迁,吸收△E1,再由高能级向低能级跃迁,放出可见光,由于紫外线光子能量大于可见光,故△E1>△E2,
故选D
(2)解:甲、乙两小孩依在抛球的时候是“一分为二”的过程,接球的过程是“合二为一”的过程.
(1)甲、乙两小孩及两车组成的系统总动量沿甲车的运动方向,甲不断抛球、乙接球后,当甲和小车与乙和小车具有共同速度时,可保证刚好不撞.设共同速度为V,则:
M1V1-M2V1=(M1+M2)V
v=1.5m/s
(2)这一过程中乙小孩接球的动量变化为:△P=30×6-30×(-1.5)=225(kg?m/s)
每一个小球被乙接收后,到最终的动量变化为△P1=16.5×1-1.5×1=15(kg?m/s)
故小球个数为 N=
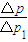 =15
=15答:①两车的速度各为1.5m/s
②甲总共抛出了15个小球.
点评:(1)本题考查原子跃迁与能级能量变化及辐射或光子能量的关系.要明确色光间的波长及频率关系.
(2)解决问题首先要清楚研究对象的运动过程.利用动量守恒定律解题,一定注意状态的变化和状态的分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

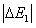 和
和 ,下列关于原子这两次跃迁的说法中正确的是( )
,下列关于原子这两次跃迁的说法中正确的是( )
 和
和 ,下列关于原子这两次跃迁的说法中正确的是( )
,下列关于原子这两次跃迁的说法中正确的是( )