题目内容
如图所示，L为薄凸透镜，点光源S位于L的主光轴上，它到L的距离为36cm；M为一与主光轴垂直的挡光圆板，其圆心在主光轴上，它到L的距离为12cm；P为光屏，到L的距离为30cm。现看到P上有一与挡光板同样大小的圆形暗区ab。求透镜的焦距。
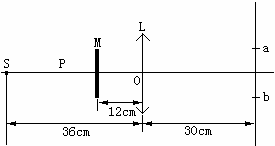
解：光屏上的暗区是由于挡光圆板挡住部分光线而形成的。因而从点光源S经挡光圆板边缘（譬如图中的c点）射到透镜上H点的光线ScH，经透镜折射后，出射光线应经过暗区的边缘的某点。这点可以是暗区的边缘点a，也可以是暗区的另一边缘点b。也就是说符合要求的像点有两点：S1'、S2'。
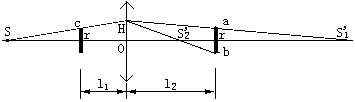
先求与像点S1'相应的焦距f1。
设r表示圆板与暗区的半径，以u表示物距，v1表示像距，
/r=u/（u-l1） ①
/r=v1/（v1-l2） ②
由成像公式，得：1/u+1/v1=1/f1 ③
解①、②、③式得：f1=25.7cm ④
再求与像点S2'相应的焦距f2，以v2表示像距，
/r=v2/（l2-v2） ⑤
由成像公式，得：1/u+1/v2=1/f2 ⑥
解①、⑤、⑥式得：f2=12cm ⑦
练习册系列答案
相关题目
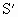处。现在在L与
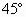角，则下面关于S的像的说法中正确的是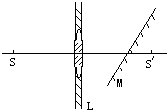
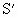处。现在在L与
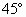角，则下面关于S的像的说法中正确的是
