题目内容
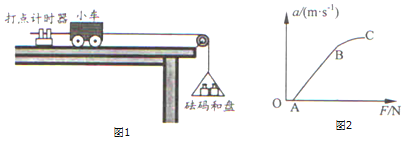
【题目】如图，一质量M＝3．0 kg、足够长的木板B放在光滑的水平面上，其上表面放置质量m＝1．0kg的小木块A，A、B均处于静止状态，A与B间的动摩擦因数μ＝0．30，且最大静摩擦力与滑动摩擦力大小相等。现给木块A施加一随时间t变化的水平力F＝kt （k＝2．0 N/s），取g＝10 m/s2。
（1）若木板B固定，则经过多少时间木块A开始滑动？
（2）若木板B固定，求t2＝2．0 s时木块A的加速度大小。
（3）若木板B不固定，求t3＝1．0 s时木块A受到的摩擦力大小。
【答案】（1）1．5s（2）1 m/s2（3）1．5 N
【解析】
试题分析：（1）当木板固定时，A开始滑动瞬间，水平力F与最大静摩擦力大小相等，
则：F＝f＝μmg，
设经过t1时间A开始滑动，则： 
。
（2）t＝2 s时，有：F＝kt＝2×2 N＝4 N，
F－μmg＝ma
a＝1 m/s2。
（3）在t＝1 s时水平外力为：F＝kt＝2×1 N＝2 N 由于此时外力小于最大静摩擦力，两者一定不发生相对滑动，故一起做匀加速运动
以整体为研究对象，有牛顿第二定律可得：F＝（m＋M）a′，a′＝0．5 m/s2
对A受力分析为：F－f＝ma′，
f＝F－ma′＝（2－1×0．5）N＝1．5 N
练习册系列答案
相关题目
