题目内容
如图所示,在场强大小为E的匀强电场中,一根不可伸长的绝缘细线一端拴一个质量为m电荷量为q的带负电小球,另一端固定在O点。把小球拉到使细线水平的位置A,然后将小球由静止释放,小球沿弧线运动到细线与水平成θ=60°的位置B时速度为零。以下说法正确的是( )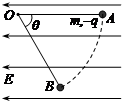
A.小球重力与电场力的关系是mg=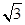 Eq Eq |
B.小球重力与电场力的关系是Eq=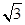 mg mg |
C.球在B点时,细线拉力为T=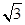 mg mg |
| D.球在B点时,细线拉力为T=2Eq |
BC
解析试题分析:方法一、小球从A运动到B的过程中,重力和电场力做功,动能的变化量为零,根据动能定理及几何知识得: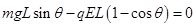 ,解得
,解得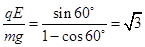 ,故B正确,A错误;小球到达B点时速度为零,向心力为零,则沿细线方向合力为零,此时对小球受力分析可知:
,故B正确,A错误;小球到达B点时速度为零,向心力为零,则沿细线方向合力为零,此时对小球受力分析可知: ,解得细线拉力
,解得细线拉力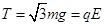 ,故C正确,D错误.所以选BC.
,故C正确,D错误.所以选BC.
方法二、类比单摆,小球从A点静止释放,运动到B点速度为0,说明弧AB的中点是运动的最低点,对小球进行受力分析,小球处在弧线中点位置时切线方向合力为零,根据对称性可知,此时细线与水平方向夹角恰为30°,根据三角函数关系可得: ,化简可知
,化简可知 ,故A错误,B正确;小球到达B点时速度为零,向心力为零,则沿细线方向合力为零,此时对小球受力分析可知:
,故A错误,B正确;小球到达B点时速度为零,向心力为零,则沿细线方向合力为零,此时对小球受力分析可知: ,解得细线拉力
,解得细线拉力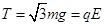 ,故C正确,D错误.所以选BC.
,故C正确,D错误.所以选BC.
考点:本题考查牛顿第二定律的应用、力的合成与分解的运用、动能定理的应用和向心力的相关知识.

如图1为伽利略研究自由落体运动实验的示意图,让小球由倾角为θ的光滑斜面滑下,然后在不同的θ角条件下进行多次实验,最后推理出自由落体运动是一种匀加速直线运动。分析该实验可知,小球对斜面的压力、小球运动的加速度和重力加速度与各自最大值的比值y随θ变化的图像分别对应图2中的( )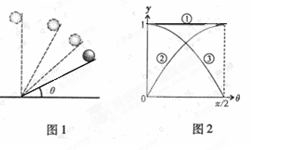
| A.①、②和③ | B.③、②和① | C.②、③和① | D.③、①和② |
如图所示,光滑球质量m,在图甲中是细线与斜面平行,图乙中是细线沿水平方向,小球均是静止状态,则甲、乙两种情况下,斜面对小球的支持力之比为( ) 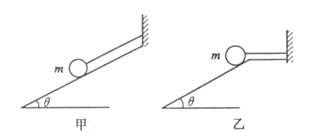
| A.1:1 | B.cos2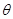 :1 :1 | C.1:cos2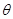 | D.sin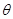 :cos :cos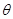 |
重50N的物体放在水平地面上,今用30N的竖直向上的力提物体,则物体所受的合力为( )
| A.20N,向下 | B.50N,向上 | C.30N,向下 | D.0 |
下列物理量在运算过程中遵循平行四边形定则的有
| A.路程 | B.速度 | C.力 | D.质量 |
一个质量为2kg的物体,在六个恒定的共点力作用下处于平衡状态.现同时撤去大小分别为15N和20N的两个力而其余力保持不变,关于此后该物体运动的说法中正确的是
| A.一定做匀变速直线运动,加速度大小可能是5m/s2 |
| B.一定做匀变速运动,加速度大小可能是15m/s2 |
| C.可能做匀减速直线运动,加速度大小是2m/s2 |
| D.可能做匀速圆周运动,向心加速度大小可能是5m/s2 |
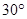 角,则每根支架中承受的压力大小为( )
角,则每根支架中承受的压力大小为( )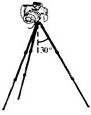
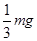
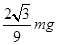

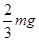
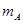 、
、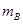 且
且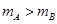 ,整个系统处于静止状态.滑轮的质量和一切摩擦均不计,如果绳一端由Q点缓慢地向左移到P点,整个系统重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角
,整个系统处于静止状态.滑轮的质量和一切摩擦均不计,如果绳一端由Q点缓慢地向左移到P点,整个系统重新平衡后,物体A的高度和两滑轮间绳与水平方向的夹角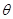 变化情况是 ( )
变化情况是 ( ) 
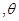 角变大
角变大