题目内容
11. 如图所示,长为l的细线一端固定在O点,另一端栓一质量为m的小球,让小球在水平面内做匀速圆周运动时,摆线与竖直方向成θ角,此时细绳的拉力为$\frac{mg}{cosθ}$,小球运动的线速度为$\sqrt{gltanθsinθ}$.
如图所示,长为l的细线一端固定在O点,另一端栓一质量为m的小球,让小球在水平面内做匀速圆周运动时,摆线与竖直方向成θ角,此时细绳的拉力为$\frac{mg}{cosθ}$,小球运动的线速度为$\sqrt{gltanθsinθ}$.
分析 小球在重力和拉力的合力作用下做匀速圆周运动,靠两个力的合力提供向心力,根据牛顿第二定律求出拉力和线速度.
解答 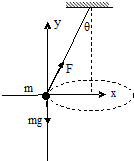 解:小球的受力分析如图所示,根据牛顿第二定律得:
解:小球的受力分析如图所示,根据牛顿第二定律得:
沿y轴方向有:Fcosθ-mg=0…①
解得:F=$\frac{mg}{cosθ}$…②
沿x轴方向有:Fsinθ=m$\frac{{v}^{2}}{R}$…③
又 R=lsinθ…④
联立②③④式得:
v=$\sqrt{gltanθsinθ}$
故答案为:$\frac{mg}{cosθ}$,$\sqrt{gltanθsinθ}$.
点评 解决本题的关键搞清小球做圆周运动向心力的来源,运用牛顿第二定律进行求解.注意小球圆周运动的半径不是l.

练习册系列答案
相关题目
2. 谷神星--小行星带中最大的行星之一,处在火星与木星轨道之间.假设各行星只受到太阳的引力,并绕太阳做匀速圆周运动,如图所示,下列说法正确的是( )
谷神星--小行星带中最大的行星之一,处在火星与木星轨道之间.假设各行星只受到太阳的引力,并绕太阳做匀速圆周运动,如图所示,下列说法正确的是( )
 谷神星--小行星带中最大的行星之一,处在火星与木星轨道之间.假设各行星只受到太阳的引力,并绕太阳做匀速圆周运动,如图所示,下列说法正确的是( )
谷神星--小行星带中最大的行星之一,处在火星与木星轨道之间.假设各行星只受到太阳的引力,并绕太阳做匀速圆周运动,如图所示,下列说法正确的是( )| A. | 太阳对谷神星和对地球的引力大小相同 | |
| B. | 谷神星绕太阳运动的周期小于一年 | |
| C. | 谷神星绕太阳运动的周期大于一年 | |
| D. | 谷神星做圆周运动的线速度值大于地球公转的线速度值 |
19.以下说法中正确的是( )
| A. | 瞬时速度可以看成是极短时间内的平均速度 | |
| B. | 物体做变速直线运动,平均速度就平均速率 | |
| C. | 物体做变速直线运动,平均速度就是物体通过的路程与所用时间的比值 | |
| D. | 做变速直线运动的物体在某段时间内的平均速度,一定和物体在这段时间首尾时刻的瞬时速度平均值相等 |
6. 如图所示,物体m与水平圆盘保持相对静止,并随盘一起绕竖直轴做匀速圆周运动,下列说法正确的是( )
如图所示,物体m与水平圆盘保持相对静止,并随盘一起绕竖直轴做匀速圆周运动,下列说法正确的是( )
 如图所示,物体m与水平圆盘保持相对静止,并随盘一起绕竖直轴做匀速圆周运动,下列说法正确的是( )
如图所示,物体m与水平圆盘保持相对静止,并随盘一起绕竖直轴做匀速圆周运动,下列说法正确的是( )| A. | 物体受重力、支持力、静摩擦力和向心力的作用 | |
| B. | 物体所受的摩擦力的方向始终指向圆心O | |
| C. | 物体所受重力和支持力是一对平衡力 | |
| D. | 摩擦力是使物体做匀速圆周运动的向心力 |
3. 如表是用单摆测重力加速度实验中获得的有关数据:
如表是用单摆测重力加速度实验中获得的有关数据:
(1)利用上面的数据,在坐标图中作出L-T2图象;
(2)根据图象可知,当地的重力加速度g=9.86m/s2;
(3)若取T2=5.2s2时,摆长Ll=1.30m.
 如表是用单摆测重力加速度实验中获得的有关数据:
如表是用单摆测重力加速度实验中获得的有关数据:| 摆长L/m | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
| 周期T2/s2 | 1.61 | 2.39 | 3.22 | 4.0 | 4.81 |
(2)根据图象可知,当地的重力加速度g=9.86m/s2;
(3)若取T2=5.2s2时,摆长Ll=1.30m.
20. 如图1所示,物块A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块A沿斜面下滑的v-t图象如图2所示,则下列说法中正确的是( )
如图1所示,物块A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块A沿斜面下滑的v-t图象如图2所示,则下列说法中正确的是( )
 如图1所示,物块A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块A沿斜面下滑的v-t图象如图2所示,则下列说法中正确的是( )
如图1所示,物块A正从斜面体B上沿斜面下滑,而斜面体在水平面上始终保持静止,物块A沿斜面下滑的v-t图象如图2所示,则下列说法中正确的是( )| A. | 物块A在沿斜面下滑的过程中受到两个力的作用 | |
| B. | 物块A在沿斜面下滑的过程中受到三个力的作用 | |
| C. | 地面对斜面体B的支持力等于物体A和B的重力之和 | |
| D. | 地面对斜面体B有水平向左的摩擦力作用 |
1.关于静电场,下列说法正确的是( )
| A. | 电势为零的物体,可能带电 | |
| B. | 不带电的物体,电势一定为零 | |
| C. | 在电场中电势相等的地方,场强也一定相等 | |
| D. | 电荷在电场中电势高的地方,具有的电势能一定大 |
 如图所示,磁流体发电机的极板相距d=0.2m,极板间有垂直于纸面向里的匀强磁场,B=1.0T.外电路中可变负载电阻R用导线与极板相连.电离气体以速率v=1100m/s沿极板射入,极板间电离气体等效内阻r=0.1Ω,试求此发电机的电动势及最大输出功率.
如图所示,磁流体发电机的极板相距d=0.2m,极板间有垂直于纸面向里的匀强磁场,B=1.0T.外电路中可变负载电阻R用导线与极板相连.电离气体以速率v=1100m/s沿极板射入,极板间电离气体等效内阻r=0.1Ω,试求此发电机的电动势及最大输出功率.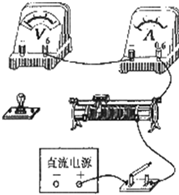 在描绘小灯泡伏安特性曲线的实验中,提供的实验器材有:
在描绘小灯泡伏安特性曲线的实验中,提供的实验器材有: