题目内容
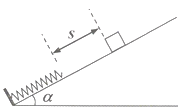
【题目】如图所示，倾角为仅的固定斜面下端固定一挡板，一劲度系数为K的轻弹簧下端固定在挡板上。现将一质量为m的小物块从斜面上离弹簧上端距离为s，由静止释放，已知物块与斜面间的动摩擦因数为μ（μ< tana），物块下滑过程中的最大动能为Ekm，则小物块从释放到运动至最低点的过程中，下列说法中正确的是
A. 物块的最大动能Ekm等于对应过程中重力与摩擦力对物块做功之和
B. 弹簧的最大弹性势能等于整个过程中重力与摩擦力对物块做功之和
C. 当物块的最大动能为Ekm时，弹簧的压缩量
D. 若将物块从离弹簧上端2s的斜面处由静止释放，则下滑过程中物块的最大动能一定等于2Ekm
【答案】BC
【解析】物块的最大动能Ekm等于对应过程中重力、摩擦力和弹簧的弹力对物块做功之和，选项A错误；当物块运动到最低端速度为零时弹性势能最大，故弹簧的最大弹性势能等于整个过程中重力与摩擦力对物块做功之和，选项B正确；当物块的最大动能为Ekm时，此时满足
，解得：
，选项C正确；若将物块从离弹簧上端2s的斜面处由静止释放，下滑过程中物块动能最大的位置不变，弹性势能不变，设为Ep．此位置弹簧的压缩量为x．根据功能关系可得：将物块从离弹簧上端s的斜面处由静止释放，下滑过程中物块的最大动能为 Ekm=mg（s+x）sinα-μmg（s+x）cosα-Ep．
将物块从离弹簧上端2s的斜面处由静止释放，下滑过程中物块的最大动能为 Ekm′=mg（2s+x）sinα-μmg（2s+x）cosα-Ep．
而2Ekm=mg（2s+2x）sinα-μmg（2s+2x）cosα-2Ep．=[mg（2s+x）sinα-μmg（2s+x）cosα-Ep]+[mgxsinα-μmgxcosα-Ep]=Ekm′+[mgxsinα-μmgxcosα-Ep]
由于在物块接触弹簧到动能最大的过程中，物块的重力势能转化为内能和物块的动能，则根据功能关系可得：mgxsinα-μmgxcosα＞Ep，即mgxsinα-μmgxcosα-Ep＞0，所以得Ekm′＜2Ekm．故D错误．故选：BC.
