Question

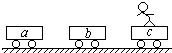如图所示，三辆相同的平板小车a、b、c成一直线排列，静止在光滑水平地面上，c车上一个小孩跳到b车上，接着又立即从b车跳到a车上，小孩跳离c车和b车时对地水平速度相同，他跳到a车上没有走动便相对a车保持静止，此后（　　）

A．a、c两车运动速率相等

B．a、b两车的运动速率相等

C．三辆车的速率关系为v_c＞v_a＞v_b

D．a、c两辆车的运动方向一定相反

Answer 1

分析：题中人与a、b、c组成的系统水平方向不受外力，系统的水平方向动量守恒，分三个过程，分别由动量守恒定律分析人与三车速率关系．

解答：解：若人跳离b、c车时速度为v，由动量守恒定律
人跳离c车的过程，有 0=-M_车v_c+m_人v，
人跳上和跳离b过程，有 m_人v=-M_车v_b+m_人v，
人跳上a车过程，有 m_人v=（M_车+m_人）?v_a，
所以：v_c=

m人v

M车

，v_b=0，v_a=

m人v

M车+m人

．
即：v_c＞v_a＞v_b，并且v_c与v_a方向相反．故ABD错误，C正确．
故选：C

点评：本题运用动量守恒定律分析人与三车速度关系，这个结果与人跳跃多少次没有关系，只要人最后落在a车上，a车的速率就小于c车的速率．