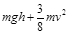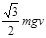题目内容
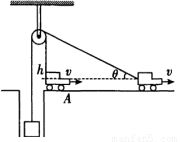
如图汽车通过轻质光滑的定滑轮,将一个质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高h,开始绳绷紧滑轮两侧的绳都竖直,汽车以v向右匀速运动,运动到跟汽车连接的细绳与水平夹角为30°,则( )

A.从开始到绳与水平夹角为30°时,拉力做功mgh
B.从开始到绳与水平夹角为30°时,拉做功mgh+
 mv2
mv2C.在绳与水平夹角为30°时,拉力功率为
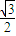 mgv
mgvD.在绳与水平夹角为30°时,绳对滑轮的作用力为
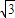 mg
mg
【答案】分析:先将汽车的速度沿着平行绳子和垂直绳子方向正交分解,得到货物速度的表达式,分析出货物的运动规律;然后根据动能定理和牛顿第二定律列式分析.
解答:解:A、B、将汽车的速度沿着平行绳子和垂直绳子方向正交分解,如图所示
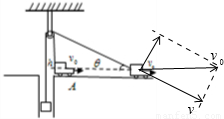
货物速度为:v=vcosθ,由于θ逐渐变小,故货物加速上升;
当θ=30°时,货物速度为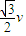 ;
;
当θ=90°时,货物速度为零;
根据功能关系,拉力的功等于货物机械能的增加量,故WF=△EP+△EK=mgh+ mv2,故A错误,B正确;
mv2,故A错误,B正确;
C、在绳与水平夹角为30°时,拉力的功率为:P=Fv,其中v=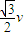 ,由于加速,拉力大于重力,故P
,由于加速,拉力大于重力,故P ,故C错误;
,故C错误;
D、由于物体加速,绳子对货物的拉力大于重力,由于两端拉力相等,夹角为60°,故合力大于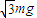 ,故D错误;
,故D错误;
故选B.
点评:本题关键将找出车的合运动与分运动,正交分解后得到货物的速度表达式,最后根据功能关系和牛顿第二定律分析讨论.
解答:解:A、B、将汽车的速度沿着平行绳子和垂直绳子方向正交分解,如图所示

货物速度为:v=vcosθ,由于θ逐渐变小,故货物加速上升;
当θ=30°时,货物速度为
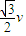 ;
;当θ=90°时,货物速度为零;
根据功能关系,拉力的功等于货物机械能的增加量,故WF=△EP+△EK=mgh+
 mv2,故A错误,B正确;
mv2,故A错误,B正确;C、在绳与水平夹角为30°时,拉力的功率为:P=Fv,其中v=
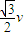 ,由于加速,拉力大于重力,故P
,由于加速,拉力大于重力,故P ,故C错误;
,故C错误;D、由于物体加速,绳子对货物的拉力大于重力,由于两端拉力相等,夹角为60°,故合力大于
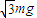 ,故D错误;
,故D错误;故选B.
点评:本题关键将找出车的合运动与分运动,正交分解后得到货物的速度表达式,最后根据功能关系和牛顿第二定律分析讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
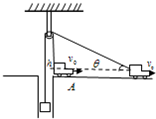
 如图所示,汽车通过轻质光滑的定滑轮,将一个质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高h,开始时物体静止,滑轮两侧的绳都竖直绷紧,汽车以v向右匀速运动,运动到跟汽车连接的细绳与水平方向的夹角为30°,则( )
如图所示,汽车通过轻质光滑的定滑轮,将一个质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高h,开始时物体静止,滑轮两侧的绳都竖直绷紧,汽车以v向右匀速运动,运动到跟汽车连接的细绳与水平方向的夹角为30°,则( )A、从开始到绳与水平方向的夹角为30°时,拉力做功大于mgh+
| ||||
| B、从开始到绳与水平方向的夹角为30°时,拉力做功大于mgh | ||||
C、在绳与水平方向的夹角为30°时,拉力功率等于
| ||||
| D、在绳与水平方向的夹角为30°时,拉力功率等于mgv |
 如图汽车通过轻质光滑的定滑轮,将一个质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高h,开始绳绷紧滑轮两侧的绳都竖直,汽车以v0向右匀速运动,运动到跟汽车连接的
如图汽车通过轻质光滑的定滑轮,将一个质量为m的物体从井中拉出,绳与汽车连接点距滑轮顶点高h,开始绳绷紧滑轮两侧的绳都竖直,汽车以v0向右匀速运动,运动到跟汽车连接的