题目内容
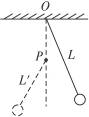
有一个单摆如图所示,其摆长为l=1.02 m,摆球的质量为m=0.1 kg,从与竖直方向夹角θ=4° 的位置无初速度释放,问: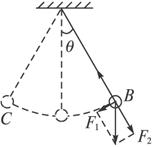
(1)已知振动的次数为n=30次,所用时间为t=60.8 s,重力加速度g等于多少?
(2)摆球的最大回复力是多少?
(3)摆球经过最低点时的速度为多大?
(4)摆球在最低点时悬线的拉力为多大?
(5)如果这个摆改为秒摆,摆长应该怎样改变?(已知:sin4°=0.069 8,cos4°=0.997 6,π=3.14)
(1)g=9.791 m/s2
(2)F1=0.068 N
(3)v=0.219 m/s
(4)FT=0.52 N
(5)Δl=l-l0=(1.02-0.993) m=0.027 m.
解析:(1)由于θ=4°<5°,所以单摆做的是简谐运动,其周期T=t/n=60.8/30 s=2.027 s,根据:
T=2π![]() ,可得:
,可得:
g=![]() =
=![]() m/s2=9.791 m/s2.
m/s2=9.791 m/s2.
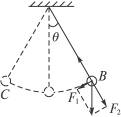
(2)当摆球处在最大位移处时即处在C或B时回复力最大,如图当摆球在B点时,进行受力分析,重力沿切线方向的分力提供向心力,所以最大回复力为:
F1=mgsin4°=0.1×9.791×0.069 8 N=0.068 N.
(3)摆球在摆动的过程中重力势能和动能相互转化,不考虑空气阻力,摆球的机械能是守恒的,其总的机械能E等于在最高点时的势能Ep或者等于在最低点时的动能Ek,设摆球在最低点时的速度等于v,则有:
![]() mv2=mgl(1-cos4°)
mv2=mgl(1-cos4°)
即有:
v=![]()
=![]() m/s=0.219 m/s
m/s=0.219 m/s
(4)在最低点时,悬线和重力的合力提供摆球的向心力,所以,由FT-mg=![]() 得,悬线的拉力为
得,悬线的拉力为
FT=mg+![]() =0.1×10 N+
=0.1×10 N+![]() N=0.52 N.
N=0.52 N.
(5)秒摆的周期T=2 s,设其摆长为l0,根据:T=2π![]() 得T∶T0=
得T∶T0=![]() ∶
∶![]() ,所以有l0=
,所以有l0=![]() =
=![]() m=0.993 m,
m=0.993 m,
所以其摆长要缩短:
Δl=l-l0=(1.02-0.993) m=0.027 m.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
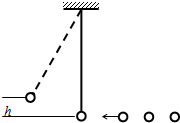 如图所示一个摆长为L=10/π2米的单摆,摆球质量为m=0.1千克,静止于平衡位置.另有质量均为m=0.1千克的小球n个与摆球在同一高度且在同一直线上,以相同的速度v=4米每秒向左运动,相邻两小球到达摆球平衡位置的时间间隔是1秒钟.每一个小球与摆球相撞后都和摆球粘在一起共同运动.(摆球和小球均视为质点,g=10m/s2)
如图所示一个摆长为L=10/π2米的单摆,摆球质量为m=0.1千克,静止于平衡位置.另有质量均为m=0.1千克的小球n个与摆球在同一高度且在同一直线上,以相同的速度v=4米每秒向左运动,相邻两小球到达摆球平衡位置的时间间隔是1秒钟.每一个小球与摆球相撞后都和摆球粘在一起共同运动.(摆球和小球均视为质点,g=10m/s2)