题目内容
【题目】一列队伍长L=120m,行进速度v1=1.6m/s.为了传达一个命令,通讯员从队伍排尾跑步赶到队伍排头,其速度v2=3m/s,然后又立即用与队伍行进速度相同大小的速度返回排尾.问:
(1)通讯员从离开队伍到重又回到排尾共需多少时间?
(2)通讯员归队处与离队处相距多远?
【答案】(1)123.2s(2)197.1m
【解析】这里有两个研究对象:通讯员和行进中的队伍,两者都作匀速直线运动,其运动示意图如图所示.设队伍原位置为AB,通讯员从排尾赶到排头时,排头已到位置A',所用时间为t,通讯员返回排尾时,排头的位置为A″,所用时间为t′.在时间t内,通讯员与队伍位移之差等于L;在时间t′内, 通讯员与队伍位移大小之和等于L.
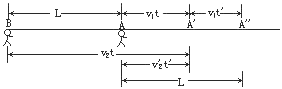
(1)通讯员从排尾赶到排头时,有关系式:v2t-v1t=L ①
设通讯员从排头返回排尾的速度为v2′,其值为v2′=v1= 1.6m/s,又有关系式:
v1t'+v'2t'=2v1t'=L ②
联立两式,得通讯员从离开队伍(排尾)到重新返回排尾共需时间: ![]()
(2)通讯员归队处与离队处相隔距离就是整个队伍在同样时间内行进的距离,即
s'=v1T=1.6×123.2m=197.1m

 小题狂做系列答案
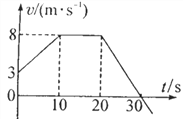
小题狂做系列答案【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点。其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为0.10s。
(1)试根据纸带上各个计数点间的距离,计算出打下B、C、D、E、F 5个点时小车的瞬时速度,并将各个速度值填入表中。(要求保留三位有效数字)
![]()
vB | vC | vD | vE | vF | |
数值/(m·s-1) | ___ | ___ | ___ | ___ | ___ |
(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并在图中画出小车的瞬时速度随时间变化的关系图线________。