题目内容
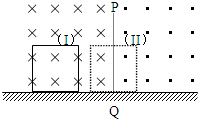 在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,如图.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从如图实线(I)位置开始向右运动,当线框运动到分别有一半面积在两个磁场中的如图(II)位置时,线框的速度为
在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,如图.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从如图实线(I)位置开始向右运动,当线框运动到分别有一半面积在两个磁场中的如图(II)位置时,线框的速度为| v |
| 2 |
分析:线框中产生的感应电动势为E=2Ba?
v,由P=
求出电功率.
线框的动能转化为电能,根据能量守恒定律求解电能.
安培力F=BIa、I=
,线框所受的合外力为2F,根据牛顿第二定律求解加速度.根据q=
,求解电量.
| 1 |
| 2 |
| E2 |
| R |
线框的动能转化为电能,根据能量守恒定律求解电能.
安培力F=BIa、I=
| E |
| R |
| △Φ |
| R |
解答:解:A、线框中产生的感应电动势为E=2Ba?
v=Bav,线框中的电功率为P=
=
.故A正确.
B、根据能量守恒定律得:线框中产生的电能为Q=
mv2-
m(
)2=
mv2.故B正确.
C、线框所受的安培力的合力为F=2BIa=2Ba?
=2
牛顿第二定律得,a=
=
.故C错误.
D、在位置Ⅱ时,线框的磁通量为零,线框磁通量的变化量△Φ=Ba2,此过程中通过线框截面的电量为q=
=
.故D错误.
故选AB
| 1 |
| 2 |
| E2 |
| R |
| B2a2v2 |
| R |
B、根据能量守恒定律得:线框中产生的电能为Q=
| 1 |
| 2 |
| 1 |
| 2 |
| v |
| 2 |
| 3 |
| 8 |
C、线框所受的安培力的合力为F=2BIa=2Ba?
| Bav |
| R |
| B2a2v |
| R |
牛顿第二定律得,a=
| F |
| m |
| 2B2a2v |
| mR |
D、在位置Ⅱ时,线框的磁通量为零,线框磁通量的变化量△Φ=Ba2,此过程中通过线框截面的电量为q=
| △Φ |
| R |
| Ba2 |
| R |
故选AB
点评:本题中线框左右两边都切割磁感线产生感应电动势,总电动势为E=2Ba?
v=Bav,不等于Ba?
.根据能量守恒和牛顿运动定律研究电磁感应中力学问题,是常用的基本规律.
| 1 |
| 2 |
| v |
| 2 |

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
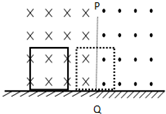 在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,如图.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为
在光滑的水平面上方,有两个磁感应强度大小均为B,方向相反的水平匀强磁场,如图.PQ为两个磁场的边界,磁场范围足够大.一个边长为a、质量为m、电阻为R的金属正方形线框,以速度v垂直磁场方向从如图实线位置开始向右运动,当线框运动到分别有一半面积在两个磁场中时,线框的速度为


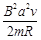






 ,则下列说法正确的是( )
,则下列说法正确的是( )



