题目内容
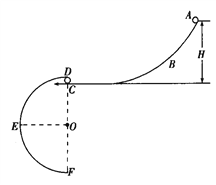
【题目】如图所示,ABC和DEF是在同一竖直平面内的两条光滑轨道,其中ABC的末端水平,DEF是半径为R的半圆形轨道,其直径DF沿竖直方向,C、D可看做重合。现有一视为质点的质量为0.2kg的小球从轨道ABC上距C点高为H的位置由静止释放。(取g=10m/![]() )
)
(1)若要使小球经C处水平进入轨道DEF后能沿轨道运动,H至少要有多高?
(2)若小球静止释放处离C点的高度h小于(1)中H的最小值,小球可击中与圆心等高的E点,求h;
(3)若小球静止释放处离C点的高度为h,小球击中与圆心等高的E时无机械能损失,击中后沿圆弧下滑,求小球对F的压力。
【答案】(1)![]() (2)h=0.1m(3)11N
(2)h=0.1m(3)11N
【解析】(1)小球从ABC轨道下滑,设到达C点时速度大小为v,
由机械能守恒定律得:mgH=![]() ①
①
要小球能竖直平面DEF内做圆周运动,在D点由题意可得:![]() ②
②
联立①②并代入数据得:H![]() 0.2m ③
0.2m ③
(2)若h<H,小球过C点只能做平抛运动,设小球经C点时速度大小为![]() ,小球能击中E点,则由机械能守恒定律得:
,小球能击中E点,则由机械能守恒定律得:![]() ④
④
且![]() ⑤
⑤
![]() ⑥
⑥
由③④⑤解得:h=0.1m
(3)设小球在F点的速度为![]() ,对小球由C到F由机械能守恒定律得:
,对小球由C到F由机械能守恒定律得:![]() ,
,
在对小球F点由向心力公式得,F-mg=![]() ,
,
解得F=5mg+![]() ,
,
由牛顿第三定律得,小球对F点的压力为11N

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目







