题目内容
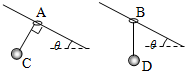（2013?崇明县二模）如图所示，两个倾角相同的滑竿上分别套有A、B两个质量均为m圆环，两个圆环上分别用细线悬吊两个质量均为M的物体C、D，当它们都沿滑竿向下滑动并保持相对静止时，A的悬线与杆垂直，B的悬线竖直向下．下列结论正确的是（ ）分析：由C球的运动情况结合曲线运动的条件得到C环受力情况并求解出加速度，然后对A环受力分析并求解A环受滑竿的作用力大小；由D球的运动情况结合曲线运动的条件得到D环受力情况并求解出加速度．
解答：解：A、C、C球做直线运动，对其受力分析，如图
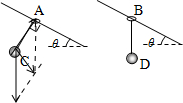
由牛顿第二定律，得到：
Mgsinθ=Ma ①
细线拉力为：T=Mgcosθ ②
再对A环受力分析，如下图
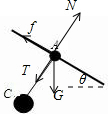
根据牛顿定律，有
mgsinθ-f=ma ③
N=mgcosθ+T ④
由①②③④解得：
f=0
N=（M+m）gcosθ
故A正确，C正确；
B、D、对D球受力分析，受重力和拉力，由于做直线运动，合力与速度在一条直线上，故合力为零，物体做匀速运动，细线拉力等于Mg；
再对B求受力分析，如图，受重力、拉力、支持力，由于做匀速运动，合力为零，故必有向后的摩擦力；
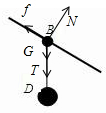
根据平衡条件，有
（M+m）gsinθ=f
N=（M+m）cosθ
故B错误，D正确；
故选ACD．
由牛顿第二定律，得到：
Mgsinθ=Ma ①
细线拉力为：T=Mgcosθ ②
再对A环受力分析，如下图
根据牛顿定律，有
mgsinθ-f=ma ③
N=mgcosθ+T ④
由①②③④解得：
f=0
N=（M+m）gcosθ
故A正确，C正确；
B、D、对D球受力分析，受重力和拉力，由于做直线运动，合力与速度在一条直线上，故合力为零，物体做匀速运动，细线拉力等于Mg；
再对B求受力分析，如图，受重力、拉力、支持力，由于做匀速运动，合力为零，故必有向后的摩擦力；
根据平衡条件，有
（M+m）gsinθ=f
N=（M+m）cosθ
故B错误，D正确；
故选ACD．
点评：本题关键灵活地选择研究对象，受力分析后根据牛顿第二定律或者平衡条件列式求解，同时要明确直线运动的条件是合力与速度共线．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2013?崇明县二模）如图所示，一质点在一恒力作用下做曲线运动，从M点运动到N点时，质点的速度方恰好改变了90°．在此过程中，质点的动能（ ）
（2013?崇明县二模）有同学利用如图（甲）所示的装置来验证力的平行四边形定则．在竖直木板上铺有白纸，固定两个光滑的滑轮A和B，将绳子打一个结点O，在三段绳上分别挂上三组钩码，每个钩码的重量相等．当系统达到平衡时，根据钩码个数读出三根绳子的拉力，回答下列问题：
（2013?崇明县二模）如图所示，正方形闭合导线框的质量可以忽略不计，将它从如图所示的位置匀速拉出匀强磁场．若第一次用0.3s时间拉出，外力所做的功为W1；第二次用0.9s时间拉出，外力所做的功为W2，则（ ）