题目内容
17. 如图所示,半径为R=1m的圆盘绕垂直于盘面的中心轴匀速转动,其正上方h=5m处沿OB方向水平抛出一小球,圆盘刚好转了一圈落在B点,则小球的初速度v=R$\sqrt{\frac{g}{2h}}$m/s圆盘转动的角速度ω=2π$\sqrt{\frac{g}{2h}}$rad/s.( g=10m/s2)
如图所示,半径为R=1m的圆盘绕垂直于盘面的中心轴匀速转动,其正上方h=5m处沿OB方向水平抛出一小球,圆盘刚好转了一圈落在B点,则小球的初速度v=R$\sqrt{\frac{g}{2h}}$m/s圆盘转动的角速度ω=2π$\sqrt{\frac{g}{2h}}$rad/s.( g=10m/s2)
分析 (1)小球做平抛运动,竖直方向做自由落体运动,已知下落的高度h可求出运动时间,水平方向做匀速直线运动,已知水平位移R,即可求出小球的初速度.
(2)小球下落的时间与圆盘转动的时间相等,可得圆盘转动的时间,考虑圆盘转动的周期性,可知圆盘转动的角度θ=n•2π,由角速度定义式求出角速度ω.
解答 解:(1)要使小球与盘只碰一次球的水平位移要为R,对平抛的小球:
水平方向:R=vt …①
竖直方向:h=$\frac{1}{2}$gt2 …②
①②联立得:v=R$\sqrt{\frac{g}{2h}}$
(2)要使小球落到B处,则小球在下落的这段时间内,B点刚好转了1圈则:
ωt=2π …③
②③联立得:ω=2π$\sqrt{\frac{g}{2h}}$ rad/s
故答案为:R$\sqrt{\frac{g}{2h}}$;2π$\sqrt{\frac{g}{2h}}$
点评 题中涉及圆周运动和平抛运动这两种不同的运动,这两种不同运动规律在解决同一问题时,常常用“时间”这一物理量把两种运动联系起来.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.某物体直线运动的位移图象如图所示,则下列说法不正确的是( )
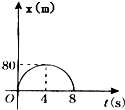

| A. | 物体运行的轨迹是抛物线 | |
| B. | 物体运行的时间为8s | |
| C. | 物体运动所能达到的最大位移为80m | |
| D. | 在8s时间内,物体的位移为零 |
5.如图,电源电动势E=3V,内阻r=0.5Ω,电阻R=1.5Ω,开关闭合时,则( )


| A. | 回路电流I=2A | B. | 外电压U外=2.25V | ||
| C. | 内电压U内=0.75V | D. | a、b两点电势差Uab=2.25V |
2. 在如图所示的电路中,电源电动势为E、内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光.当滑动变阻器的滑片向右移动时,下列判断正确的是( )
在如图所示的电路中,电源电动势为E、内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光.当滑动变阻器的滑片向右移动时,下列判断正确的是( )
 在如图所示的电路中,电源电动势为E、内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光.当滑动变阻器的滑片向右移动时,下列判断正确的是( )
在如图所示的电路中,电源电动势为E、内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光.当滑动变阻器的滑片向右移动时,下列判断正确的是( )| A. | 灯泡L将变暗 | B. | 灯泡L将变亮 | ||
| C. | 电容器C的电量将减小 | D. | 电容器C的电量将增大 |
9. 如图所示,AD表示粗细均匀的一段金属导体L,两端加上一定电压,导体中的自由电荷沿导体定向移动的速率为v,设导体的横截面积为S,导体内单位体积内的电荷数为n,每个自由电荷的电量为q,则导体中的电流强度I的表达式为( )
如图所示,AD表示粗细均匀的一段金属导体L,两端加上一定电压,导体中的自由电荷沿导体定向移动的速率为v,设导体的横截面积为S,导体内单位体积内的电荷数为n,每个自由电荷的电量为q,则导体中的电流强度I的表达式为( )
 如图所示,AD表示粗细均匀的一段金属导体L,两端加上一定电压,导体中的自由电荷沿导体定向移动的速率为v,设导体的横截面积为S,导体内单位体积内的电荷数为n,每个自由电荷的电量为q,则导体中的电流强度I的表达式为( )
如图所示,AD表示粗细均匀的一段金属导体L,两端加上一定电压,导体中的自由电荷沿导体定向移动的速率为v,设导体的横截面积为S,导体内单位体积内的电荷数为n,每个自由电荷的电量为q,则导体中的电流强度I的表达式为( )| A. | I=$\frac{sV}{nq}$ | B. | I=nqsv | C. | I=nqLv | D. | I=nLsv |
7.以下说法正确的是( )
| A. | 机械能守恒时,物体一定只受重力作用 | |
| B. | 机械能守恒时,物体一定只受重力和弹力作用 | |
| C. | 物体处于平衡状态时机械能一定守恒 | |
| D. | 物体所受的合外力不为零,其机械能也可以守恒 |