题目内容
某同学在探究摩擦力的实验中采用了如图所示的操作，将一个长方体木块放在水平桌面上，然后用一个力传感器对木块施加一个水平拉力F，并用另外一个传感器对木块的运动状态进行监测，表是她记录的实验数据．木块的重力为10．ON，重力加速度g=9.80m/s2，根据表格中的数据回答下列问题（答案保留3位有效数字）：| 实验次数 | 运动状态 | 水平拉力F/N |
| 1 | 静止 | 3.62 |
| 2 | 静止 | 4.00 |
| 3 | 静止 | 4.02 |
| 4 | 匀速 | 4.01 |
| 5 | 匀加速 | 5.01 |
| 6 | 匀加速 | 5.49 |
4.02
4.02
N；（2）木块与桌面间的动摩擦因数
0.401
0.401
；（3）实验次数6中监测到的加速度a=
1.45
1.45
m/s2．分析：（1）物体相对静止时受到的摩擦力是静摩擦力，摩擦力的最大值是最大静摩擦力，静摩擦力小于等于最大静摩擦力；
物体在拉力与摩擦力作用下静止，处于平衡状态，静摩擦力等于拉力，根据表中实验数据判断最大静摩擦力的大小；
（2）物体在水平力作用下沿水平面运动时，FN=mg，Ff=F=FNμ由此可求出滑动摩擦因数大小；
（3）根据牛顿第二定律列方程可以求出物体的加速度大小．
物体在拉力与摩擦力作用下静止，处于平衡状态，静摩擦力等于拉力，根据表中实验数据判断最大静摩擦力的大小；
（2）物体在水平力作用下沿水平面运动时，FN=mg，Ff=F=FNμ由此可求出滑动摩擦因数大小；
（3）根据牛顿第二定律列方程可以求出物体的加速度大小．
解答：解：（1）由表中实验数据可知，第3次实验时，物体受到的静摩擦力f=F=4.02N，
物体受到的静摩擦力小于等于最大静摩擦力，因此木块与桌面间的最大静摩擦力≥4.02N；
（2）木块做匀速直线运动，处于平衡状态，受到的滑动摩擦力Ff=F=4.01N，
滑动摩擦力为：Ff=FNμ ①FN=G ②
联立①②μ=
=
=0.401．
（3）由牛顿第二定律得：
F6-Ff=ma，带入数据解得：a=1.45m/s2．
故答案为：（1）4.02；（2）0.401；（3）1.45．
物体受到的静摩擦力小于等于最大静摩擦力，因此木块与桌面间的最大静摩擦力≥4.02N；
（2）木块做匀速直线运动，处于平衡状态，受到的滑动摩擦力Ff=F=4.01N，
滑动摩擦力为：Ff=FNμ ①FN=G ②
联立①②μ=
| Ff |
| G |
| 4.01N |
| 10.0N |
（3）由牛顿第二定律得：
F6-Ff=ma，带入数据解得：a=1.45m/s2．
故答案为：（1）4.02；（2）0.401；（3）1.45．
点评：滑动摩擦力大小跟压力大小、接触面粗糙程度有关，跟物体受到的拉力大小、物体的运动速度都没有关系，正确根据物体所处状态列方程求解．
练习册系列答案
相关题目
某同学在探究摩擦力的实验中采用了如图所示的操作，将一个长方体木块放在水平桌面上，然后用一个力传感器对木块施加一个水平拉力F，并用另外一个传感器对木块的运动状态进行监测，表1是她记录的实验数据．木块的重力为10.00N，重力加速度g=9.80m/s2，根据表格中的数据回答下列问题：
某同学在探究摩擦力的实验中采取了如图所示的操作，将一个长方体木块放在水平桌面上，然后用一个力传感器对木块施加一个水平拉力F，并用另外一个传感器对木块的运动状态进行监测，表1是她记录的实验数据．木块的重力为10.00N，重力加速度g=9.80m/s2，根据表格中的数据回答下列问题（答案保留3位有效数字）：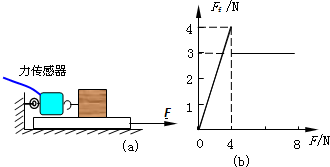
某同学在探究摩擦力的实验中采用了如图所示的操作，将木块放在水平长木板上，如图（a）所示，用力沿水平方向拉长木板，拉力从0开始逐渐增大．分别用力传感器采集拉力和木块所受到的摩擦力，并用计算机绘制出摩擦力Ff随拉力F的变化图象，如图（b）所示．已知木块质量为1.0kg，取重力加速度g=10m/s2．由上述采集的数据，请你回答下列问题：
（2011?许昌一模）（1）如图1甲所示，某同学将一端固定有滑轮的长木板水平放置在桌面上，利用钩码通过细绳水平拉小车，让小车从静止开始运动，利用打点计时器在纸带上记录小车的运动情况．如图1乙所示，其中O点为纸带上记录到的第一点，A、B、C是该同学在纸带上所取的一些点．已知打点计时器所用交流电源的频率为50Hz（打点计时器每隔0.02s打一个点），利用图中给出的数据，算出打点计时器打下B点时小车的速度大小vB=