题目内容
17.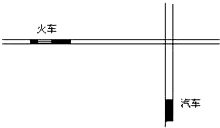 一辆长为L1=5m的汽车以v1=15m/s的速度行驶,在离铁路与公路交叉点s1=175m处,汽车司机突然发现离交叉点s2=200m处有一列长L2=300m的列车以v2=20m/s的速度行驶过来,为了避免事故的发生,汽车司机可能会采取加速通过或减速停止的措施,请就不同的措施分别计算其加速度的最小值?(不考虑司机的反应时间)
一辆长为L1=5m的汽车以v1=15m/s的速度行驶,在离铁路与公路交叉点s1=175m处,汽车司机突然发现离交叉点s2=200m处有一列长L2=300m的列车以v2=20m/s的速度行驶过来,为了避免事故的发生,汽车司机可能会采取加速通过或减速停止的措施,请就不同的措施分别计算其加速度的最小值?(不考虑司机的反应时间)
分析 若汽车匀加速冲过去,结合火车到达交叉点的时间,汽车的位移,根据位移时间公式求出汽车的最小加速度.
若汽车刹车做匀减速运动,根据火车通过交叉点的时间,结合位移公式求出刹车的加速度,结合速度时间公式判断汽车是否通过交叉点,若通过交叉点,则到达交叉点的速度必须为零,再结合速度位移公式求出汽车的最小加速度.
解答 解:若汽车先于列车通过交叉点,
则用时为:t1≤$\frac{{s}_{2}}{{v}_{2}}=\frac{200}{20}s=10s$,
而匀速的时间为:t′=$\frac{175+5}{15}s=12s$>t1,
所以汽车必须加速,设加速度为a1,则有:
v1t1+$\frac{1}{2}{a}_{1}{{t}_{1}}^{2}$≥175+5
代入数据解得:a1≥0.6m/s2
若汽车在列车之后通过交叉点,则汽车到达交叉点用时为:
t2≥$\frac{200+300}{20}s=25s$
汽车在这段时间内的位移为175m,有:
${v}_{1}{t}_{2}-\frac{1}{2}{a}_{2}{{t}_{2}}^{2}$=175m
代入数据解:得a=0.64m/s2.
此时有:v=v1-at=-1m/s
因此汽车已经在25s前冲过了交叉点,发生了交通事故,不合题意.
要使汽车安全减速,必须在小于25s的时间内汽车速度减少为零,
设汽车的加速度大小为a2,
则$\frac{{{v}_{2}}^{2}}{2{a}_{2}}$≤175,
解得:a2≥0.643m/s2
答:汽车做匀加速运动冲过去,那么汽车的加速度至少为0.6m/s2.汽车刹车做匀减速运动,那么汽车的加速度至少为0.643m/s2.
点评 解决本题的关键抓住汽车和火车的位移关系,根据时间相等,结合位移公式灵活求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.以下说法正确的是( )
| A. | 在研究黑体辐射现象时,普朗克提出了光子模型,他认为光子能量与频率成正比 | |
| B. | 光波是一种概率波,不是电磁波 | |
| C. | 电子衍射实验为物质波的概念提代供了实验验证 | |
| D. | 根据不确定关系,可以同时确定微观粒子的速度和位置,从而描绘出微观粒子的运动轨迹 |
5. 一质点自x轴原点出发,沿正方向以加速度a运动,经过t0时间速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加
一质点自x轴原点出发,沿正方向以加速度a运动,经过t0时间速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加
速度再变为-a,直到速度为-$\frac{{v}_{0}}{8}$…,其v-t图象如图所示,则下列说法正确的是( )
 一质点自x轴原点出发,沿正方向以加速度a运动,经过t0时间速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加
一质点自x轴原点出发,沿正方向以加速度a运动,经过t0时间速度变为v0,接着以-a加速度运动,当速度变为-$\frac{{v}_{0}}{2}$时,加速度又变为a,直至速度变为$\frac{{v}_{0}}{4}$时,加速度再变为-a,直到速度为-$\frac{{v}_{0}}{8}$…,其v-t图象如图所示,则下列说法正确的是( )
| A. | 质点一直沿x轴正方向运动 | |
| B. | 质点在x轴上原点O两侧往复运动 | |
| C. | 质点运动过程中离原点的最大距离大于v0t0 | |
| D. | 质点最终静止时离开原点的距离一定大于$\frac{3}{4}$v0t0 |
12. 如图所示为A、B两质点在同一直线上运动的位置-时间(x-t)图象.A质点的图象为直线,B质点的图象为过原点的抛物线,两图象交点C、D坐标如图所示.下列说法正确的是( )
如图所示为A、B两质点在同一直线上运动的位置-时间(x-t)图象.A质点的图象为直线,B质点的图象为过原点的抛物线,两图象交点C、D坐标如图所示.下列说法正确的是( )
 如图所示为A、B两质点在同一直线上运动的位置-时间(x-t)图象.A质点的图象为直线,B质点的图象为过原点的抛物线,两图象交点C、D坐标如图所示.下列说法正确的是( )
如图所示为A、B两质点在同一直线上运动的位置-时间(x-t)图象.A质点的图象为直线,B质点的图象为过原点的抛物线,两图象交点C、D坐标如图所示.下列说法正确的是( )| A. | 两次相遇的时刻分别是t1、t2 | |
| B. | 0~t1时间段内A在前 B在后,t1~t2时间段内B在前A在后 | |
| C. | 两物体速度相等的时刻一定为t1~t2时间段内的中间时刻 | |
| D. | A在B前面且离B最远时,B的位移为$\frac{{x}_{1}+{x}_{2}}{2}$ |
2.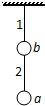 质量分别为m、2m的带电小球a、b用绝缘细线1和2悬挂,如图所示.已知两球带异种电荷,a球对线2的拉力为F,则线1产生的拉力大小为( )
质量分别为m、2m的带电小球a、b用绝缘细线1和2悬挂,如图所示.已知两球带异种电荷,a球对线2的拉力为F,则线1产生的拉力大小为( )
 质量分别为m、2m的带电小球a、b用绝缘细线1和2悬挂,如图所示.已知两球带异种电荷,a球对线2的拉力为F,则线1产生的拉力大小为( )
质量分别为m、2m的带电小球a、b用绝缘细线1和2悬挂,如图所示.已知两球带异种电荷,a球对线2的拉力为F,则线1产生的拉力大小为( )| A. | 2mg+F | B. | 3mg | C. | 3mg+F | D. | 3mg-F |
9.在如图甲所示的电路中,L1、L2、L3为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示.当开关S闭合后,电路中的总电流为0.25A,则此时( )


| A. | L2的电阻为12Ω | B. | L1消耗的电功率为0.75 W | ||
| C. | L1、L2消耗的电功率的比值大于4 | D. | L1两端的电压为L2两端电压的2倍 |
6. 一块艇要以最快时间渡过河宽为100m的河流,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )
一块艇要以最快时间渡过河宽为100m的河流,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )
 一块艇要以最快时间渡过河宽为100m的河流,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )
一块艇要以最快时间渡过河宽为100m的河流,已知快艇在静水中的速度图象如图甲所示,流水的速度图象如图乙所示,则( )| A. | 快艇的运动轨迹是直线 | B. | 快艇的运动轨迹是曲线 | ||
| C. | 快艇通过的位移为100m | D. | 快艇所用时间为20s |

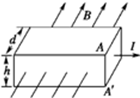 如图所示,厚度为h、宽度为d的导体板放在垂直于它的磁感应强度为B的匀强磁场中,当电流通过导体板时,在导体板的上侧面A和下侧面A′之间会产生电势差,这种现象称为霍尔效应.设电流I是由自由电子的定向流动形成的,电子的平均定向移动速度为v,电荷量为e,回答下列问题:
如图所示,厚度为h、宽度为d的导体板放在垂直于它的磁感应强度为B的匀强磁场中,当电流通过导体板时,在导体板的上侧面A和下侧面A′之间会产生电势差,这种现象称为霍尔效应.设电流I是由自由电子的定向流动形成的,电子的平均定向移动速度为v,电荷量为e,回答下列问题: