题目内容
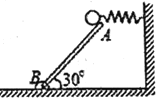
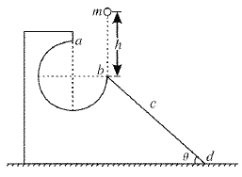
【题目】一梯形木块固定在水平面上，木块内有半径为R的圆形轨道，ab缺口正好为四分之一的圆周，bd斜面的倾角θ=45°。今将质量为m的小球在b点的正上方h=2R处由静止释放，小球恰好能从a点出射，出射后落在斜面的c点上。不计空气阻力并忽略小球每次在圆轨内从b运动到a阻力做功的差异。
（1）求bc两点间的距离；
（2）若将小球改在
处释放，小球恰好落在斜面底端d点。求小球在a点时对轨道的压力；
（3）若小球某次出射后落点与a点的水平距离为4R，求小球的释放高度h。
【答案】（1）
R；（2）
mg；（3）
【解析】
（1）由题可知，小球恰好能从a点出射，则有
解得
设c点与a点的水平距离为x，根据几何关系可知竖直方向的位移为
则有
解得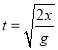
则水平位移为
解得x=2R
根据几何关系可得bc=R
（2）设小球从b运动到a克服阻力做功为W，根据动能定理有
解得
若小球从a点出射速度为
，根据动能定理有
解得
在a点，根据牛顿第二定律有
解得
根据牛顿第三定律可知，小球在a点时对轨道的压力大小为
，方向竖直向上；
(3) 若d点与a点的水平距离为
，根据几何关系可得
则有
解得
则在水平方向上有
解得x=3R
当水平位移为4R>3R时小球从a点出射速度为
，则竖直方向的位移为
，则有
解得
则在水平方向上有
解得
根据动能定理有
解得
练习册系列答案
相关题目
