题目内容
(1)一跳水运动员从离水面10m 高的平台上向上跃起,举双臂直体离开台面,此时其重心位于从手到脚全长的中点,跃起后重心升高0.45m 达到最高点,落水时身体竖直,手先入水(在此过程中运动员水平方向的运动忽略不计).从离开跳台到手触水面,他可用于完成空中动作的时间约是多少?(计算时,可以把运动员看作全部质量集中在重心的一个质点,g 取为10m/s2,(1.5)2=2.25,(1.45)2=2.1025,(1.4)2=1.96,结果保留二位有效数字)
(2)飞镖是一项时尚的运动,飞镖质量为0.01Kg,一名运动员在距离一堵竖直木板墙壁3m前投掷飞镖,求:(g=10m/s2)
①当以30m/s的水平速度投掷飞镖,飞镖插在墙壁上的位置与抛掷点的竖直距离(不考虑空气阻力)
②如果考虑空气对飞镖有阻力且只考虑水平阻力为0.2N,想飞镖仍插在墙壁原来位置上,则水平投掷速度要多大?
(2)飞镖是一项时尚的运动,飞镖质量为0.01Kg,一名运动员在距离一堵竖直木板墙壁3m前投掷飞镖,求:(g=10m/s2)
①当以30m/s的水平速度投掷飞镖,飞镖插在墙壁上的位置与抛掷点的竖直距离(不考虑空气阻力)
②如果考虑空气对飞镖有阻力且只考虑水平阻力为0.2N,想飞镖仍插在墙壁原来位置上,则水平投掷速度要多大?
分析:(1)将整个过程分为上升过程和下降过程进行求解,上升做匀减速直线运动,求出上升的时间,下落做自由落体运动,求出自由落体的时间,两个时间之和为运动员在空中完成动作的时间.
(2)竖直高度一定,时间就不变,水平方向上由原来的匀速运动变成匀减速运动,由牛顿第二定律求出水平的加速度.由于水平位移和时间不变,根据位移公式可求出此时的初速度.
(2)竖直高度一定,时间就不变,水平方向上由原来的匀速运动变成匀减速运动,由牛顿第二定律求出水平的加速度.由于水平位移和时间不变,根据位移公式可求出此时的初速度.
解答:解:(1)向上跃起运动员作竖直上抛运动,达最高点的时间,由位移公式,有h=
gt12
解得 t1=
=
s=0.3s
从最高点开始做自由落体运动H+h=
gt22
解得 t2=
=
s≈1.4s
因此,运动员从向上跃起开始算起可用于完成空中动作的时间为t=t1+t2≈1.7s
故运动员从向上跃起开始算起可用于完成空中动作的时间为1.7s.
(2)①飞镖作平抛运动,飞镖飞行时间为
t=
=0.1s
飞镖在竖直方向的位移h
由h=
gt2=0.05m
②当考虑空气水平阻力时,飞镖水平方向做匀减速运动
a=
=20m/s2
设第二次投掷飞镖速度为v′
由s=v′t-
a t2得
v′=31m/s
答:(1)运动员从向上跃起开始算起可用于完成空中动作的时间为1.7s.
(2)①当以30m/s的水平速度投掷飞镖,飞镖插在墙壁上的位置与抛掷点的竖直距离为0.05m.
②如果考虑空气对飞镖有阻力且只考虑水平阻力为0.2N,想飞镖仍插在墙壁原来位置上,则水平投掷速度应为31m/s.
| 1 |
| 2 |
解得 t1=
|
|
从最高点开始做自由落体运动H+h=
| 1 |
| 2 |
解得 t2=
|
|
因此,运动员从向上跃起开始算起可用于完成空中动作的时间为t=t1+t2≈1.7s
故运动员从向上跃起开始算起可用于完成空中动作的时间为1.7s.
(2)①飞镖作平抛运动,飞镖飞行时间为
t=
| s |
| v |
飞镖在竖直方向的位移h
由h=
| 1 |
| 2 |
②当考虑空气水平阻力时,飞镖水平方向做匀减速运动
a=
| f |
| m |
设第二次投掷飞镖速度为v′
由s=v′t-
| 1 |
| 2 |
v′=31m/s
答:(1)运动员从向上跃起开始算起可用于完成空中动作的时间为1.7s.
(2)①当以30m/s的水平速度投掷飞镖,飞镖插在墙壁上的位置与抛掷点的竖直距离为0.05m.
②如果考虑空气对飞镖有阻力且只考虑水平阻力为0.2N,想飞镖仍插在墙壁原来位置上,则水平投掷速度应为31m/s.
点评:将竖直上抛运动分解为上升过程和下降过程进行求解.因为在整个过程中加速度保持不变,整个过程做匀变速直线运动,本题也可以采取运动学公式对整个过程求解,注意矢量的方向.

练习册系列答案
相关题目
 (2012?长宁区一模)跳水运动员从高于水面H=10m的跳台自由落下,身体笔直且与水面垂直.假设运动员的质量m=50kg,其体型可等效为一长度L=1.0m、直径d=0.30m的圆柱体,略去空气阻力.运动员落水后,水的等效阻力f作用于圆柱体的下端面,f的量值随落水深度Y变化的函数曲线如图所示. 该曲线可近似看作椭圆的一部分,该椭圆的长、短轴分别与坐标轴OY和Of重合.运动员入水后受到的浮力F=ρgV (V是排开水的体积)是随着入水深度线性增加的.已知椭圆的面积公式是S=πab,水的密度ρ=1.0×103kg/m3,g取10m/s2.
(2012?长宁区一模)跳水运动员从高于水面H=10m的跳台自由落下,身体笔直且与水面垂直.假设运动员的质量m=50kg,其体型可等效为一长度L=1.0m、直径d=0.30m的圆柱体,略去空气阻力.运动员落水后,水的等效阻力f作用于圆柱体的下端面,f的量值随落水深度Y变化的函数曲线如图所示. 该曲线可近似看作椭圆的一部分,该椭圆的长、短轴分别与坐标轴OY和Of重合.运动员入水后受到的浮力F=ρgV (V是排开水的体积)是随着入水深度线性增加的.已知椭圆的面积公式是S=πab,水的密度ρ=1.0×103kg/m3,g取10m/s2.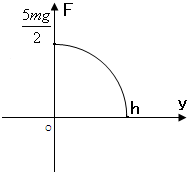 跳水运动员从脚底高于水面H=10米的跳台自由落下,假设运动员的质量m=60千克,其体形可等效为一长度L=1.0米、直径d=0.30米的圆柱体,略去空气阻力.运动员入水后,水的等效阻力F(非浮力)作用于圆柱体的下端面,F的数值随入水深度y变化的函数曲线如图.该曲线可近似看圆周的
跳水运动员从脚底高于水面H=10米的跳台自由落下,假设运动员的质量m=60千克,其体形可等效为一长度L=1.0米、直径d=0.30米的圆柱体,略去空气阻力.运动员入水后,水的等效阻力F(非浮力)作用于圆柱体的下端面,F的数值随入水深度y变化的函数曲线如图.该曲线可近似看圆周的