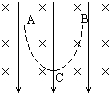题目内容
【题目】如图所示(a),在倾角为30°的斜面上固定一光滑金属导轨CDEFG,OH∥CD∥FG,∠DEF=60,CD=DE=EF=FG=AB/2=L,一根质量为m的导体棒AB在电机的牵引下,以恒定的速度v0沿OH方向从斜面底部开始运动,滑上导轨并到达斜面顶端,AB⊥OH,金属导轨的CD、FG段电阻不计,DEF段与AB棒材料、横截面积均相同,单位长度电阻为r,O是AB棒的中点,整个斜面处在垂直斜面向上磁感应强度为B的匀强磁场中。求:
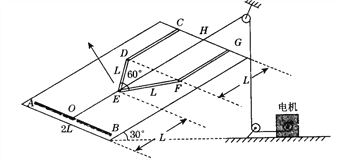
(1)导体棒在导轨上滑行时电路中的电流的大小;
(2)导体棒运动到DF位置时AB两端的电压;
(3)将导体棒从低端拉到顶端电机对外做的功;
(4)若AB到顶端后,控制电机的功率,使导体棒AB沿斜面向下从静止开始做匀加速直线运动,加速度大小始终为a,一直滑到斜面底端,则此过程中电机提供的牵引力随时间如何变化?(运动过程中AB棒的合力始终沿斜面向下)。
【答案】(1)![]() (2)
(2)![]() (3)
(3)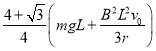
【解析】试题分析:导体棒在导轨上滑行时,根据感应电动势公式得出电动势与有效长度的关系,由题意得到电阻与有效长度的关系,根据欧姆定律得到导体棒在导轨DEF上滑动时电路中电流的大小;AB两端的电压等于AD、DF、FB三段感应电动势之和。AD、FB两段电压等于感应电动势,DF段根据电压分配求出;根据功能关系可知,导体棒从底端拉到斜面顶端过程电机对杆做的功等于导体棒增加的重力势能与电路产生的热量之和,AB棒在DEF上滑动时产生的电热Q1,数值上等于克服安培力做的功;分三段讨论牵引力随时间的变化情况:CDEF导轨上、DEF导轨上和OE段.导体棒做匀加速运动,加速度为a.根据牛顿第二定律、运动学公式及各段感应电流、安培力的表达式结合得到牵引力随时间的变化情况。
(1)导体棒在导轨上匀速滑行时,设AB棒等效切割长度为l,则
导体棒在导轨上E=BLv0
回路总电阻为R总=3Lr
则感应电流为: ![]()
联立解得: ![]()
AB棒滑到DF处时,AB两端的电压UBA=UDA+UFD+UBF
又有:UDA+UBF=BLv0
可得: ![]()
则有: ![]()
(3)导体棒从低端拉到顶端电机做的功: ![]()
增加的重力势能 ![]()
AB棒在DEF轨道上滑动时产生的热量 ![]() ,此过程中,电流I不变,所以F安∝S,故
,此过程中,电流I不变,所以F安∝S,故 ![]()
AB棒在CDEF导轨上滑动时产生的热量,电流不变,电阻不变,所以
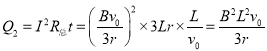
所以: 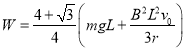
(4)分三段讨论牵引力随时间的变化情况
Ⅰ:CDEF导轨上运动牵引力为F1,根据牛顿第二定律: ![]()
其中: ![]() ,
, ![]() ,
, ![]()
联立可得: ![]()
Ⅱ:DEF导轨上运动牵引力为F2,则![]()
![]() ,
, ![]() ,
, ![]()
位移为: ![]()
所以 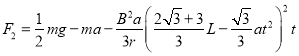
Ⅲ:OE段运动牵引力F3,不随时间变化,则![]()