题目内容
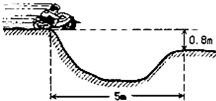
 如图所示,在水平路上骑摩托车的人,遇到一个壕沟,沟两岸高低差0.8m水平间距5m,(忽略空气阻力,g取10m/s2)求:摩托车要安全越过这个壕沟,水平飞出的速度至少多大?且落地时它的速度方向与地面的夹角的正切值是多大?
如图所示,在水平路上骑摩托车的人,遇到一个壕沟,沟两岸高低差0.8m水平间距5m,(忽略空气阻力,g取10m/s2)求:摩托车要安全越过这个壕沟,水平飞出的速度至少多大?且落地时它的速度方向与地面的夹角的正切值是多大?分析:由两边的高度差可求得摩托车在空中的飞行时间;人应在这段时间内飞到对岸;则可知摩托车的水平位移和竖直位移;由平抛运动的规律可求得飞出时的速度及落地时的速度方向.
解答:解:由h=
gt2可得;
车在空中飞行时间t=
=0.4s;
要想安全飞过壕沟,则飞行距离至少为5m,故水平分速度v=
=12.5m/s;
落地时的竖直分速度vy=gt=4m/s;
合速度与水平方向的夹角tanθ=
=0.32;
答:水平分速度为12.5m/s;落地时它的速度方向与地面的夹角的正切值是0.32.
| 1 |
| 2 |
车在空中飞行时间t=
|
要想安全飞过壕沟,则飞行距离至少为5m,故水平分速度v=
| x |
| t |
落地时的竖直分速度vy=gt=4m/s;
合速度与水平方向的夹角tanθ=
| vy |
| gt |
答:水平分速度为12.5m/s;落地时它的速度方向与地面的夹角的正切值是0.32.
点评:本题考查平抛运动在生活中的应用,要注意平抛运动在水平方向为匀速直线运动,竖直方向为自由落体.

练习册系列答案
相关题目
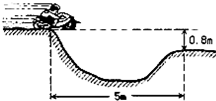
 如图所示,在水平路上匀速行驶的骑摩托车,遇到一个壕沟,壕沟宽5m,高度差0.8m,若摩托车刚好越过这个壕沟.(g=10m/s2)求:
如图所示,在水平路上匀速行驶的骑摩托车,遇到一个壕沟,壕沟宽5m,高度差0.8m,若摩托车刚好越过这个壕沟.(g=10m/s2)求: